题目内容
17.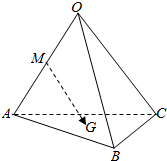 如图所示,已知空间四边形OABC,其对角线为OB,AC,M是边OA的中点,G是△ABC的重心,用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.
如图所示,已知空间四边形OABC,其对角线为OB,AC,M是边OA的中点,G是△ABC的重心,用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.
分析 根据所给的图形和一组基底,从起点O出发,把不是基底中的向量,用是基底的向量来表示,就可以得到结论.
解答  解:延长AG交BC与点N,则N是BC的中点,
解:延长AG交BC与点N,则N是BC的中点,
$\overrightarrow{AN}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{2}$($\overrightarrow{OB}$-$\overrightarrow{OA}$+$\overrightarrow{OC}$-$\overrightarrow{OA}$)=$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$-2$\overrightarrow{OA}$),
$\overrightarrow{MG}$=$\overrightarrow{MA}$+$\overrightarrow{AG}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{2}{3}$×$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$-2$\overrightarrow{OA}$)=$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.
故答案为:$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.
点评 本题考查向量的基本定理及其意义,解题时注意方法,即从要表示的向量的起点出发,沿着空间图形的棱走到终点,若出现不是基底中的向量的情况,再重复这个过程.

 名校课堂系列答案
名校课堂系列答案| A. | (0,$\frac{3}{4}$) | B. | ($\frac{3}{4}$,2] | C. | [0,$\frac{3}{4}$) | D. | ($\frac{1}{2}$,2) |
| A. | {1,2,3,5} | B. | {2,3} | C. | {2} | D. | {1,2} |
| 工序时间原料 | 粗加工 | 精加工 |
| 原料A | 9 | 15 |
| 原料B | 6 | 21 |
| A. | 36 | B. | 42 | C. | 45 | D. | 51 |