题目内容

7．求函数f（x）=log2（-x2+4x-3）的单调增区间．

分析 求函数的定义域，由二次函数的单调性和复合函数的单调性可得．

解答 解：由对数有意义可得t=-x2+4x-3＞0，
解得1＜x＜3，可得函数的定义域为（1，3），
又∵二次函数t=-x2+4x-3在（-∞，2）单调递增，
∴由复合函数单调性和定义域可得单调增区间为（1，2）

点评 本题考查对数函数的图象和性质，涉及二次函数的单调性和复合函数的单调性，属基础题．

练习册系列答案
相关题目
17．已知圆G：x2+y2-x-$\sqrt{3}$y=0，经过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的右焦点F及上顶点B，过圆外一点（m，0）（m＞a）倾斜角为$\frac{3π}{4}$的直线l交椭圆于C，D两点．
（1）求椭圆的方程；
（2）若右焦点F在以线段CD为直径的圆E的内部，求m的取值范围．
18．已知实数m，n满足n=2$\sqrt{1-\frac{{m}^{2}}{5}}$，则$\sqrt{{m}^{2}+（n-1）^{2}}$+$\sqrt{（m-1）^{2}+{n}^{2}}$的最小值是$\sqrt{2}$．
15．已知f（x）=x2-2|x|（x∈R）．
（Ⅰ）若方程f（x）=kx有三个解，试求实数k的取值范围；
（Ⅱ）求m，n（m＜n），使函数f（x）的定义域与值域均为[m，n]．
2．已知x＞0，y＞0，且x+y＞2，求证：$\frac{1+y}{x}$＜2或$\frac{1+x}{y}$＜2．
12．有F列四个命题：
①命题“若|x|≥2，则x≥2或x≤-2”的否命题；
②命题“面积相等的三角形全等”的否命题；
③命题“若m≤1，则x2-2x+m=0有实根”的逆否命题；
④命题“若A∩B=B，则A?B”的逆否命题．
其中是真命题的是①②③（填上你认为正确的命题的序号）．
19．数列{an}的通项公式为an=an-1+lg2n（a＞0），则此数列的前n项和为$\left\{\begin{array}{l}{\frac{lg2}{2}{n}^{2}+n（1+\frac{1}{2}lg2），a=1}\\{\frac{1-{a}^{n}}{1-a}+\frac{n（n-1）}{2}lg2，a＞0且a≠1}\end{array}\right.$．
16．如图所示，当参数λ分别取λ1，λ2时，函数f（x）=$\frac{x}{2-λx}$（x≥0）的部分图象分别对应曲线C1，C2，则有（　　）
A．0＜λ1＜λ2B．0＜λ2＜λ1C．λ1＜λ2＜0D．λ2＜λ1＜0
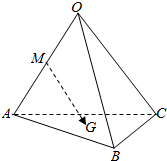17．如图所示，已知空间四边形OABC，其对角线为OB，AC，M是边OA的中点，G是△ABC的重心，用基向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网