题目内容
11.已知函数f(x)=$\left\{\begin{array}{l}{x+1,0≤x≤1}\\{(\frac{1}{2})^{x}+1,x>1}\end{array}\right.$,设a>b≥0,若f(a)=f(b),则b•f(a)的取值范围是( )| A. | (0,$\frac{3}{4}$) | B. | ($\frac{3}{4}$,2] | C. | [0,$\frac{3}{4}$) | D. | ($\frac{1}{2}$,2) |
分析 先作出函数f(x)的图象,根据f(a)=f(b)的关系,确定a,b以及f(a)的取值范围,利用数形结合以及不等式的性质进行求解即可.
解答  解:由函数f(x)的解析式作出其图象如图,则当0≤x≤1时,函数f(x)为增函数,且1≤f(x)≤2,
解:由函数f(x)的解析式作出其图象如图,则当0≤x≤1时,函数f(x)为增函数,且1≤f(x)≤2,
当x>1时,函数f(x)为减函数,且1<f(x)<$\frac{3}{2}$,
由x+1=$\frac{3}{2}$,得x=$\frac{1}{2}$,
所以,若满足a>b≥0时,f(a)=f(b),
必有b∈[0,$\frac{1}{2}$),a∈[1,+∞),1<f(a)<$\frac{3}{2}$,
则0<b•f(a)<$\frac{1}{2}×\frac{3}{2}$=$\frac{3}{4}$,
由不等式的可乘积性得:b•f(a)∈(0,$\frac{3}{4}$),
故选:A.
点评 本题考查分段函数的应用,根据条件作出函数f(x)的图象,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
20.已知lga+lgb=lg2,$\frac{a}{{a}^{2}+2}$+$\frac{b}{{b}^{2}+2}$的最大值是( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
3.函数y=x2+x在x=1到x=1+△x之间的平均变化率为( )
| A. | △x+2 | B. | 2△x+(△x)2 | C. | △x+3 | D. | 3△x+(△x)2 |
20.若m是函数f(x)=$\sqrt{x}$-2x+2的一个零点,且x1∈(0,m),x2∈(m,+∞),则f(x1),f(x2),f(m)的大小关系为( )
| A. | f(x1)<f(m)<f(x2) | B. | f(m)<f(x2)<f(x1) | C. | f(m)<f(x1)<f(x2) | D. | f(x2)<f(m)<f(x1) |
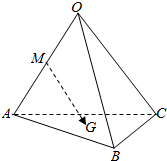 如图所示,已知空间四边形OABC,其对角线为OB,AC,M是边OA的中点,G是△ABC的重心,用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.
如图所示,已知空间四边形OABC,其对角线为OB,AC,M是边OA的中点,G是△ABC的重心,用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.