题目内容
9．现需要把A，B两件玉石原料各加工为一件工艺品，师父甲带领徒弟乙完成这件事，每件原料徒弟先粗加工，再由师父精加工，然后完成制作，两件原料每道工序所需时间（单位：小时）如下：| 工序时间原料 | 粗加工 | 精加工 |
| 原料A | 9 | 15 |
| 原料B | 6 | 21 |
| A． | 36 | B． | 42 | C． | 45 | D． | 51 |
分析 由题意分析结合最优化思想可得加工方案，可得最短时间．
解答 解：由题意可得交货日期最短即耽误工期最少，
故先让徒弟加工原料B需6小时，再由师傅精加工需21小时，
师傅精加工期间徒弟用9小时可把原料A粗加工，
然后再由师傅精加工A需15小时，
故最短时间为6+21+15=42
故选：B
点评 本题考查最优化问题，属基础题．
练习册系列答案
相关题目
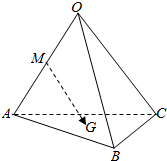如图所示，已知空间四边形OABC，其对角线为OB，AC，M是边OA的中点，G是△ABC的重心，用基向量$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$．
20．若m是函数f（x）=$\sqrt{x}$-2x+2的一个零点，且x1∈（0，m），x2∈（m，+∞），则f（x1），f（x2），f（m）的大小关系为（ ）
| A． | f（x1）＜f（m）＜f（x2） | B． | f（m）＜f（x2）＜f（x1） | C． | f（m）＜f（x1）＜f（x2） | D． | f（x2）＜f（m）＜f（x1） |
17．已知$y=\sqrt{2016}$，则y′=（ ）
| A． | $\frac{1}{{2\sqrt{2016}}}$ | B． | $-\frac{1}{{2\sqrt{2016}}}$ | C． | $\frac{2016}{{\sqrt{2016}}}$ | D． | 0 |