题目内容
8.画出函数y=|($\frac{1}{2}$)|x|-$\frac{1}{2}$|的图象,并利用图象回答:k为何值时,方程|($\frac{1}{2}$)|x|-$\frac{1}{2}$|=k无解?有一解?有两解?分析 取绝对值,化为分段函数,根据函数的奇偶性得到图象,由图象即可得到k的值.
解答  解:该函数为偶函数,只有画出x轴右边的图象即可得到函数y的图象,
解:该函数为偶函数,只有画出x轴右边的图象即可得到函数y的图象,
当0<x<1时,y=($\frac{1}{2}$)x-$\frac{1}{2}$,
当x>1时,y=-($\frac{1}{2}$)x+$\frac{1}{2}$,
其图象如图所示,
由图象可知,当k<0或k>1时,方程|($\frac{1}{2}$)|x|-$\frac{1}{2}$|=k无解,
当k<0或k>1时,方程|($\frac{1}{2}$)|x|-$\frac{1}{2}$|=k无解,
当k=1时,方程|($\frac{1}{2}$)|x|-$\frac{1}{2}$|=k有一解,
当k=0时,方程|($\frac{1}{2}$)|x|-$\frac{1}{2}$|=k有两解.
点评 本题绝对值函数的图象和画法和图象的识别,方程根的问题,属于中档题.

练习册系列答案
相关题目
16. 如图所示,当参数λ分别取λ1,λ2时,函数f(x)=$\frac{x}{2-λx}$(x≥0)的部分图象分别对应曲线C1,C2,则有( )
如图所示,当参数λ分别取λ1,λ2时,函数f(x)=$\frac{x}{2-λx}$(x≥0)的部分图象分别对应曲线C1,C2,则有( )
 如图所示,当参数λ分别取λ1,λ2时,函数f(x)=$\frac{x}{2-λx}$(x≥0)的部分图象分别对应曲线C1,C2,则有( )
如图所示,当参数λ分别取λ1,λ2时,函数f(x)=$\frac{x}{2-λx}$(x≥0)的部分图象分别对应曲线C1,C2,则有( )| A. | 0<λ1<λ2 | B. | 0<λ2<λ1 | C. | λ1<λ2<0 | D. | λ2<λ1<0 |
13.已知Sn是数列{an}的前n项和,若Sn=1-an,则数列{an}是( )
| A. | 等差数列 | B. | 递减的等比数列 | C. | 递增的等比数列 | D. | 不是等比数列 |
20.已知lga+lgb=lg2,$\frac{a}{{a}^{2}+2}$+$\frac{b}{{b}^{2}+2}$的最大值是( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
20.若m是函数f(x)=$\sqrt{x}$-2x+2的一个零点,且x1∈(0,m),x2∈(m,+∞),则f(x1),f(x2),f(m)的大小关系为( )
| A. | f(x1)<f(m)<f(x2) | B. | f(m)<f(x2)<f(x1) | C. | f(m)<f(x1)<f(x2) | D. | f(x2)<f(m)<f(x1) |
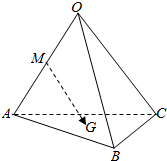 如图所示,已知空间四边形OABC,其对角线为OB,AC,M是边OA的中点,G是△ABC的重心,用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.
如图所示,已知空间四边形OABC,其对角线为OB,AC,M是边OA的中点,G是△ABC的重心,用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{MG}$的表达式为$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$-$\frac{1}{6}$$\overrightarrow{OA}$.