题目内容
已知
,
,
是两两垂直的单位向量,
=2
-
+
,
=
+
-3
,则
•
= .
| i |
| j |
| k |
| a |
| i |
| j |
| k |
| b |
| i |
| j |
| k |
| a |
| b |
考点:平面向量数量积的运算
专题:空间向量及应用
分析:利用数量积定义即可得出.
解答:
解:∵
,
,
是两两垂直的单位向量,
=2
-
+
,
=
+
-3
,
∴
=(2,-1,1),
=(1,1,-3),
∴
•
=2-1-3=-2,
故答案为:-2
| i |
| j |
| k |
| a |
| i |
| j |
| k |
| b |
| i |
| j |
| k |
∴
| a |
| b |
∴
| a |
| b |
故答案为:-2
点评:熟练掌握数量积运算法则是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若M={x|x>1},N={x|x≥a},且N⊆M,则( )
| A、a≤1 | B、a≥1 |
| C、a<1 | D、a>1 |
已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点F的距离为5,该抛物线的顶点在直线MF上的射影为点P,则点P的坐标为( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
 如图,在正四棱锥P-ABCD中,底面为正方形,AB=2,VP-ABCD=
如图,在正四棱锥P-ABCD中,底面为正方形,AB=2,VP-ABCD=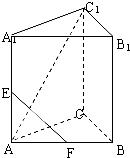 如图,在正三棱柱ABC-A1B1C1中,AC=2,AC1与底面成60°角,E、F分别为AA1、AB的中点.
如图,在正三棱柱ABC-A1B1C1中,AC=2,AC1与底面成60°角,E、F分别为AA1、AB的中点.