题目内容
已知向量a=(m,-2),b=(4,-2m),条件p:a∥b,条件q:m=2,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据向量平行的性质,求出关于p的m的值,根据充分必要条件的定义进行判断即可.
解答:
解:若a∥b,则-2m2+8=0,解得:m=±2,
∴P:m=±2,而q:m=2,
∴p是q的必要不充分条件,
故选:B.
∴P:m=±2,而q:m=2,
∴p是q的必要不充分条件,
故选:B.
点评:本题考查了向量问题,考查了充分必要条件,本题属于基础题.

练习册系列答案
相关题目
已知O是坐标原点,点A(-2,1),若点M(x,y)为平面区域
上的一个动点,则
•
的取值范围是( )
|
| OA |
| OM |
| A、[0,1] |
| B、[0,2] |
| C、[-1,0] |
| D、[-1,2] |
设复数z的共轭复数为
,若(2+i)z=3-i,则z•
的值为( )
. |
| z |
. |
| z |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
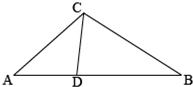 如图,在△ABC中,D为AB边上一点,DA=DC,已知B=
如图,在△ABC中,D为AB边上一点,DA=DC,已知B=