题目内容
12.函数f(x)=-(x-5)|x|的单调递增区间是(0,$\frac{5}{2}$).分析 对x进行分段讨论,取绝对值,利用二次函数的性质求解.
解答 解:函数f(x)=-(x-5)|x|,
当x≥0时,可得f(x)=-x2+5x,其对称轴x=$\frac{5}{2}$,在(0,$\frac{5}{2}$)是单调递增.
当x<0时,可得f(x)=x2-5x,其对称轴x=$\frac{5}{2}$,在(-∞,0)是单调递减.
∴函数f(x)=-(x-5)|x|的单调递增区间为(0,$\frac{5}{2}$).
故答案为(0,$\frac{5}{2}$).
点评 本题考查了绝对值的化简和单调性的讨论.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
3.已知sin(3π+α)=2sin$({\frac{3π}{2}+α})$,求下列各式的值:
(1)$\frac{2sinα-3cosα}{4sinα-9cosα}$;
(2)sin2α+sin 2α.
(1)$\frac{2sinα-3cosα}{4sinα-9cosα}$;
(2)sin2α+sin 2α.
7.下列命题正确的是( )
| A. | 若a2>b2,则a>b | B. | 若ac>bc,则a>b | C. | 若$\frac{1}{a}>\frac{1}{b},则a<b$ | D. | 若$\sqrt{a}<\sqrt{b},则a<b$ |
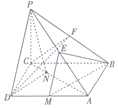 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点. 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.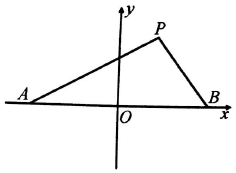 如图,设点A,B的坐标分别为(-$\sqrt{3}$,0),($\sqrt{3}$,0),直线AP,BP相交于点P,且它们的斜率之积为-$\frac{2}{3}$.
如图,设点A,B的坐标分别为(-$\sqrt{3}$,0),($\sqrt{3}$,0),直线AP,BP相交于点P,且它们的斜率之积为-$\frac{2}{3}$.