题目内容
4.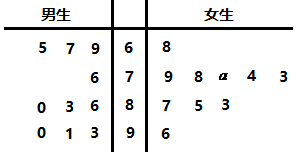 某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).
某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).已知男、女生成绩的平均值相同.
(1)求a的值;
(2)从成绩高于86分的学生中任意抽取3名学生,求恰有2名学生是女生的概率.
分析 (1)分别求出男生的平均成绩和女生的平均成绩,得到关于a的方程,解出即可;
(2)列出从成绩高于86分的学生中任意抽取3名学生所有抽取的结果以及满足条件的结果,从而求出满足条件的概率即可.
解答 解:(1)男生的平均成绩为$\overline{x}$=$\frac{1}{10}$(3×90+3×80+70+3×60+1+3+3+6+6+9+7+5)=80,
女生的平均成绩为$\overline{y}$=$\frac{1}{10}$(90+3×80+5×70+60+6+7+5+3+9+8+a+4+3+8)=$\frac{793+a}{10}$,
由题意得:$\overline{x}$=$\overline{y}$,即$\frac{793+a}{10}$=80,解得:a=7;
(2)从成绩高于86分的学生中任意抽取3名学生,
所有抽取的结果是(96,93,91),(96,93,90),(96,93,87),(96,91,90),
(96,91,87),(96,09,87),(93,91,90),(93,91,87),(93,90,87),(91,90,87)
共10种情况.
其中恰有2名学生是女生的结果是(96,93,87),(96,91,87),(96,90,87)共3种情况.
所以从成绩高于8(6分)的学生中抽取了3名学生恰有2名是女生的概率P=$\frac{3}{10}$.
点评 本题考查了平均数的求法,考查条件概率问题,是一道基础题.

练习册系列答案
相关题目
14.设变量x,y满足约束条件:$\left\{\begin{array}{l}{y≥x}\\{x+2y≤2}\\{x≥-2}\end{array}\right.$,则z=$\frac{y+2}{x+2}$ 的( )
| A. | 最大值为-$\frac{1}{2}$ | B. | 最小值为-$\frac{1}{2}$ | C. | 最大值为1 | D. | 最小值为1 |
12.函数f(x)=$\frac{x}{1-x}$+$\sqrt{x+1}$的定义域是( )
| A. | [-1,+∞) | B. | (-∞,-1) | C. | (-∞,+∞) | D. | [-1,1)∪(1,+∞) |
16.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知a=7,c=5,则$\frac{sinA}{sinC}$的值是( )
| A. | $\frac{7}{5}$ | B. | $\frac{5}{7}$ | C. | $±\frac{7}{12}$ | D. | $\frac{5}{12}$ |
13.已知集合A={x|x2-5x+4≤0},B={-1,0,1,2,3},则A∩B=( )
| A. | {-1,0,1} | B. | {0,1,2} | C. | {1,2,3} | D. | {1,2,3,4} |