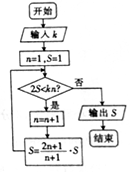
题目内容
18.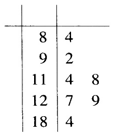 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:| AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)若甲地每年同期的空气质量状况变化不大,请根据统计数据估计2017年11月甲地空气质量为良的天数(结果精确到天);
(Ⅱ)从甲地的这7个数据中任意抽取2个,求AQI均超过100的概率.
分析 (Ⅰ)这7天中甲地空气质量为良的天数为2天,由此能估计2017年11月甲地空气质量为良的天数.
(Ⅱ)甲地的这7个数据中任意抽取2个,基本事件总数n=${C}_{7}^{2}$=21,甲地的这7个数据中AQI超过100的数据有5个,抽取的2天的AQI均超过100,包含的基本事件个数m=${C}_{5}^{2}=10$,由此能求出AQI均超过100的概率.
解答 解:(Ⅰ)由7天的AQI数据的茎叶图,知:
这7天中甲地空气质量为良的天数为2天,
由此估计2017年11月甲地空气质量为良的天数为:
$30×\frac{2}{7}$=$\frac{60}{7}$≈9(天).
(Ⅱ)甲地的这7个数据中任意抽取2个,基本事件总数n=${C}_{7}^{2}$=21,
甲地的这7个数据中AQI超过100的数据有5个,
∴抽取的2天的AQI均超过100,包含的基本事件个数m=${C}_{5}^{2}=10$,
∴AQI均超过100的概率p=$\frac{m}{n}=\frac{10}{21}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
9.已知0<α<$\frac{π}{2}$,若m=lg$\sqrt{1+cosα}$,n=lg$\frac{1}{\sqrt{1-cosα}}$,则sinα等于( )
| A. | 10m+n | B. | 10m-n | C. | 10mn | D. | 10${\;}^{\frac{m}{n}}$ |
7.2${\;}^{\frac{1}{2}+lo{g}_{2}9}$的值是( )
| A. | 12$\sqrt{2}$ | B. | 9+$\sqrt{2}$ | C. | 9$\sqrt{2}$ | D. | 8+$\sqrt{2}$ |
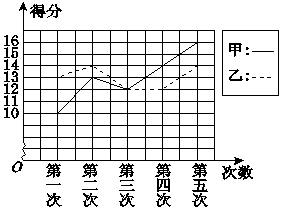 甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.
甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.