题目内容
8．已知直线l：kx-y+1-2k=0（k∈R）过定点P，则点P的坐标为（2，1）．分析 kx-y+1-2k=0，化为y-1=k（x-2），即可得出直线经过的定点．
解答 解：kx-y+1-2k=0，化为y-1=k（x-2），
∵k∈R，∴$\left\{\begin{array}{l}{x-2=0}\\{y-1=0}\end{array}\right.$，解得x=2，y=1．
∴点P的坐标为（2，1）．
故答案为（2，1）．
点评 本题考查了直线方程及其直线经过定点，考查了推理能力与计算能力，比较基础．
练习册系列答案
名校课堂系列答案
相关题目
19．已知向量$\overrightarrow a\;，\;\;\overrightarrow b$都是非零向量，“$\overrightarrow a•\overrightarrow b=|{\overrightarrow a}|•|{\overrightarrow b}|$”是“$\overrightarrow a∥\overrightarrow b$”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充分必要条件 | D． | 既非充分也非必要条件 |
16．
进位制是人们为了计数和运算方便而约定的记数系统，在日常生活中，我们最熟悉、最常用的是十进制．如图是实现将某进制数a化为十进制数b的程序框图，若输入的k=2，a=110，n=3，则输出的b=（ ）
进位制是人们为了计数和运算方便而约定的记数系统，在日常生活中，我们最熟悉、最常用的是十进制．如图是实现将某进制数a化为十进制数b的程序框图，若输入的k=2，a=110，n=3，则输出的b=（ ）| A． | 14 | B． | 12 | C． | 6 | D． | 3 |
18．
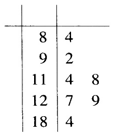空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的指数．空气质量分分级与AQI大小关系如表所示：
某环保人士从2016年11月甲地的AQI记录数据轴，随机抽取了7天的AQI数据，用茎叶图记录如下：
（Ⅰ）若甲地每年同期的空气质量状况变化不大，请根据统计数据估计2017年11月甲地空气质量为良的天数（结果精确到天）；
（Ⅱ）从甲地的这7个数据中任意抽取2个，求AQI均超过100的概率．
空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的指数．空气质量分分级与AQI大小关系如表所示：| AQI | 0～50 | 51～100 | 101～150 | 151～200 | 201～300 | 300以上 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
（Ⅰ）若甲地每年同期的空气质量状况变化不大，请根据统计数据估计2017年11月甲地空气质量为良的天数（结果精确到天）；
（Ⅱ）从甲地的这7个数据中任意抽取2个，求AQI均超过100的概率．