题目内容
8.已知函数$f(x)=a-\frac{1}{{{2^x}+1}}$.(1)试确定a的值,使f(x)为奇函数;
(2)判断函数f(x)的单调性,并用定义法证明.
分析 (1)利用f(0)=0,确定a的值,使f(x)为奇函数;
(2)利用函数单调性的定义进行证明即可.
解答 解:(1)由题意,f(0)=a-$\frac{1}{2}$=0,∴a=$\frac{1}{2}$,
f(-x)=a-$\frac{1}{{2}^{-x}+1}$;
∵f(x)+f(-x)=a-$\frac{1}{{2}^{x}+1}$+a-$\frac{1}{{2}^{-x}+1}$=2a-$\frac{{2}^{x}+1}{{2}^{x}+1}$=2a-1;
∴经检验a=$\frac{1}{2}$,f(x)为奇函数;
(2)函数f(x)在定义域R内单调递增.
任意设两个实数x1,x2,且x1<x2,
则f(x1)-f(x2)=$\frac{{2}^{{x}_{1}}-{2}^{{x}_{2}}}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$,
∵x1<x2,
∴${2}^{{x}_{1}}$-${2}^{{x}_{2}}$<0,(1+${2}^{{x}_{1}}$)(1+${2}^{{x}_{2}}$)>0
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在定义域R内单调递增.
点评 本题主要考查奇函数的定义,考查函数单调性的判断,利用函数单调性的定义是解决此类问题的基本方法.

练习册系列答案
相关题目
18.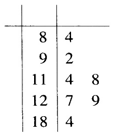 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:
某环保人士从2016年11月甲地的AQI记录数据轴,随机抽取了7天的AQI数据,用茎叶图记录如下:
(Ⅰ)若甲地每年同期的空气质量状况变化不大,请根据统计数据估计2017年11月甲地空气质量为良的天数(结果精确到天);
(Ⅱ)从甲地的这7个数据中任意抽取2个,求AQI均超过100的概率.
 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:| AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)若甲地每年同期的空气质量状况变化不大,请根据统计数据估计2017年11月甲地空气质量为良的天数(结果精确到天);
(Ⅱ)从甲地的这7个数据中任意抽取2个,求AQI均超过100的概率.
20.某市拟招商引资兴建一化工园区,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如表所示:
(Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在30岁以上的人有多少人被抽取;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
| 支持 | 保留 | 不支持 | |
| 30岁以下 | 900 | 120 | 280 |
| 30岁以上(含30岁) | 300 | 260 | 140 |
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
17.已知数列{an}的前n项和为Sn,且Sn=2an-1,则$\frac{S_6}{a_6}$=( )
| A. | $\frac{63}{32}$ | B. | $\frac{31}{16}$ | C. | $\frac{123}{64}$ | D. | $\frac{127}{128}$ |
18.计算log232•log327=(( )
| A. | 12 | B. | 10 | C. | 15 | D. | 18 |
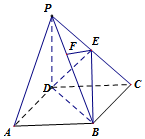 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.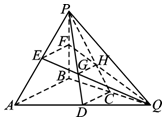 已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.
已知:在三棱锥P-ABQ 中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则多面体ADGE-BCHF的体积与三棱锥P-ABQ体积之比是$\frac{11}{18}$.