题目内容
11.6颗颜色不同的钻石,可穿成几种钻石圈?分析 根据环状排列没有首尾之分,将n个元素围城的环状排列剪开看成n个元素排成一排,即共有Ann种排法.由于n个元素共有n种不同的剪法,则环状排列共有$\frac{{A}_{n}^{n}}{n}$种排法,而钻石圈没有反正,故可以求出答案.
解答 解:因为由于环状排列没有首尾之分,将n个元素围城的环状排列剪开看成n个元素排成一排,即共有Ann种种排法.由于n个元素共有n种不同的剪法,则环状排列共有有$\frac{{A}_{n}^{n}}{n}$种种排法,而钻石圈没有反正,
故6颗颜色不同的钻石,可穿成$\frac{{A}_{6}^{6}}{6×2}$=60种不同的钻石圈.
点评 本题主要考查了环状排列问题,本题的关键是由于6个元素共有6种不同的剪法,钻石圈没有反正,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
6.已知α是第二象限角,且$sin({\frac{π}{2}+α})=-\frac{{\sqrt{5}}}{5}$,则$\frac{{{{cos}^3}α+sinα}}{{cos({α-\frac{π}{4}})}}$=( )
| A. | $-\frac{{11\sqrt{2}}}{15}$ | B. | $-\frac{{9\sqrt{2}}}{5}$ | C. | $\frac{{9\sqrt{2}}}{5}$ | D. | $\frac{{11\sqrt{2}}}{15}$ |
1.(1+x)+(1+x)2+(1+x)3+(1+x)4+…+(1+x)49展开式中x3的系数是( )
| A. | ${C}_{51}^{3}$ | B. | ${C}_{50}^{4}$ | C. | ${C}_{51}^{4}$ | D. | ${C}_{47}^{4}$ |
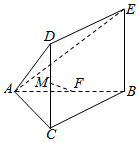 在如图所示的空间几何体中,AC⊥BC,四边形DCBE为矩形,点F,M分别为AB,CD的中点.
在如图所示的空间几何体中,AC⊥BC,四边形DCBE为矩形,点F,M分别为AB,CD的中点.