题目内容
函数y=tan（x-2）的最小正周期是（ ）
| A、π | ||
| B、2π | ||
C、
| ||
| D、1 |
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：根据函数y=tan（ωx+φ）的周期为为T=
，得出结论．
| π |
| ω |
解答：
解：函数y=tan（x-2）的最小正周期为T=
=π，
故选：A．
| π |
| ω |
故选：A．
点评：本题主要考查三角函数的周期性，利用了函数y=tan（ωx+φ）的周期为T=
，属于基础题．
| π |
| ω |
练习册系列答案
相关题目
已知三角形的三条边成公差为2的等差数列，且它的最大角的正弦值为
，则这个三角形的面积是（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若b为a，c的等比中项，则函数y=ax2+bx+c的零点个数是（ ）
| A、0 | B、1 |
| C、2 | D、A、B、C都有可能 |
已知向量
=（-2，-1），
=（λ，1），则
与
夹角θ为钝角时，λ的取值范围为（ ）
| a |
| b |
| a |
| b |
A、λ＞
| ||
B、λ＜-
| ||
C、λ＞-
| ||
| D、无法确定 |
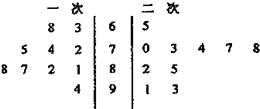如图是某同学一学期两次考试成绩的茎叶图，现从该同学两次考试成绩中各取一科成绩，则这两科成绩都在80分以上的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|