题目内容
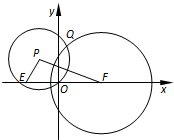 如图,已知O(0,0),E(-
如图,已知O(0,0),E(-| 3 |
| 3 |
| 3 |
(Ⅰ)求点P的轨迹方程;
(Ⅱ)证明:点Q到直线PF的距离为定值,并求此值.
考点:圆与圆锥曲线的综合,圆与圆的位置关系及其判定,椭圆的定义
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ) 根据|PE|+|PF|=4>|EF|,利用椭圆定义知,点P的轨迹是以E,F为焦点,4为长轴长的椭圆,从而可求点P的轨迹方程;
(Ⅱ)P(x0,y0),Q(x1,y1),T(x2,y2),由题意知,圆P的方程为(x-x0)2+(y-y0)2=x02+y02,可得(x0-
)x1+y0 y1-1=0,同理(x0-
)x2+y0 y2-1=0,从而可得直线QT的方程,连接PF交QT于H,则PF⊥QT,求出|FH|,即可求点Q到直线PF的距离.
(Ⅱ)P(x0,y0),Q(x1,y1),T(x2,y2),由题意知,圆P的方程为(x-x0)2+(y-y0)2=x02+y02,可得(x0-
| 3 |
| 3 |
解答:
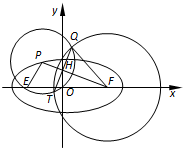 (Ⅰ)解:∵|PE|+|PF|=4>|EF|,
(Ⅰ)解:∵|PE|+|PF|=4>|EF|,
∴根据椭圆定义知,点P的轨迹是以E,F为焦点,4为长轴长的椭圆.
设P(x,y),则点P的轨迹方程为
+y2=1. …(6分)
(Ⅱ)证明:设圆P与圆F的另一个公共点为T,并设P(x0,y0),Q(x1,y1),T(x2,y2),
则由题意知,圆P的方程为(x-x0)2+(y-y0)2=x02+y02.
又Q为圆P与圆F的一个公共点,故
所以(x0-
)x1+y0 y1-1=0.
同理(x0-
)x2+y0 y2-1=0.
因此直线QT的方程为(x0-
)x+y0y-1=0.
连接PF交QT于H,则PF⊥QT.
设|QH|=d (d>0),则在直角△QHF中|FH|=
.
又
+
=1,故|FH|=
=2×
=2.
在直角△QHF中d=
=1.
所以点Q到直线PF的距离为1. …(15分)
 (Ⅰ)解:∵|PE|+|PF|=4>|EF|,
(Ⅰ)解:∵|PE|+|PF|=4>|EF|,∴根据椭圆定义知,点P的轨迹是以E,F为焦点,4为长轴长的椭圆.
设P(x,y),则点P的轨迹方程为
| x2 |
| 4 |
(Ⅱ)证明:设圆P与圆F的另一个公共点为T,并设P(x0,y0),Q(x1,y1),T(x2,y2),
则由题意知,圆P的方程为(x-x0)2+(y-y0)2=x02+y02.
又Q为圆P与圆F的一个公共点,故
|
所以(x0-
| 3 |
同理(x0-
| 3 |
因此直线QT的方程为(x0-
| 3 |
连接PF交QT于H,则PF⊥QT.
设|QH|=d (d>0),则在直角△QHF中|FH|=
|
| ||||||
|
又
| ||
| 4 |
| y | 2 0 |
|
| ||||||||
|
|
| ||||||
|
在直角△QHF中d=
| 5-|FH|2 |
所以点Q到直线PF的距离为1. …(15分)
点评:本题主要考查椭圆的定义、圆与圆的位置关系、点到直线距离、直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
在平面直角坐标系xOy中,已知
=(-1,t),
=(1,1),若∠ABO=90°,则实数t的值为( )
| OA |
| OB |
| A、3 | B、1 | C、0 | D、-1 |
若b为a,c的等比中项,则函数y=ax2+bx+c的零点个数是( )
| A、0 | B、1 |
| C、2 | D、A、B、C都有可能 |
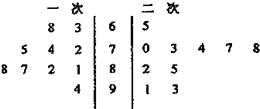 如图是某同学一学期两次考试成绩的茎叶图,现从该同学两次考试成绩中各取一科成绩,则这两科成绩都在80分以上的概率为( )
如图是某同学一学期两次考试成绩的茎叶图,现从该同学两次考试成绩中各取一科成绩,则这两科成绩都在80分以上的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|