题目内容
3.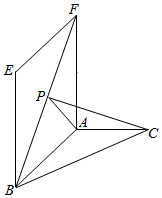 如图所示,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2$\sqrt{3}$,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一点,PF=3.
如图所示,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2$\sqrt{3}$,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一点,PF=3.(1)证明:FB⊥平面PAC;
(2)求异面直线PC与AB所成的角的余弦值.
分析 (Ⅰ)以A为原点,向量$\overrightarrow{AB}$、$\overrightarrow{AC}$、$\overrightarrow{AF}$的方向为x,y,z轴的正方向,建立空间直角坐标系利用向量法能证明FB⊥平面APC.
(Ⅱ)先求出$\overrightarrow{AB}$=(2,0,0),$\overrightarrow{PC}$=(-$\frac{3}{2}$,2,-$\frac{\sqrt{3}}{2}$),由此利用向量法能求出异面直线PC与AB所成的角的余弦值.
解答  证明:(Ⅰ)以A为原点,向量$\overrightarrow{AB}$、$\overrightarrow{AC}$、$\overrightarrow{AF}$的方向为x,y,z轴的正方向,建立空间直角坐标系,
证明:(Ⅰ)以A为原点,向量$\overrightarrow{AB}$、$\overrightarrow{AC}$、$\overrightarrow{AF}$的方向为x,y,z轴的正方向,建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(0,2,0),F(0,0,2$\sqrt{3}$),
∵BF=$\sqrt{A{B}^{2}+A{F}^{2}}$=4,PF=3,∴AN=AB×$\frac{PF}{PB}$=2×$\frac{3}{4}$=$\frac{3}{2}$,PN=$\frac{AF}{4}$=$\frac{\sqrt{3}}{2}$,
∴P($\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$),$\overrightarrow{FB}$=(2,0,-2$\sqrt{3}$),
$\overrightarrow{AC}$=(0,2,0),$\overrightarrow{AP}$=($\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$),
∵$\overrightarrow{FB}•\overrightarrow{AC}$=0,∴$\overrightarrow{FB}•\overrightarrow{AC}$,∵FB⊥AC,FB⊥AP,AC∩AP=A,
∴FB⊥平面APC.
解:(Ⅱ)∵$\overrightarrow{AB}$=(2,0,0),$\overrightarrow{PC}$=(-$\frac{3}{2}$,2,-$\frac{\sqrt{3}}{2}$),
记$\overrightarrow{AB}$与$\overrightarrow{PC}$夹角为θ,
则|cosθ|=$\frac{|\overrightarrow{AB}•\overrightarrow{PC}|}{|\overrightarrow{AB}|•|\overrightarrow{PC}|}$=$\frac{|-3|}{2\sqrt{7}}$=$\frac{3\sqrt{7}}{14}$.
∴异面直线PC与AB所成的角的余弦值为$\frac{3\sqrt{7}}{14}$.
点评 本题考查线面垂直的证明,考查异面直线所成角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | -$\frac{1}{6}$ | B. | -6 | C. | 6 | D. | $\frac{1}{6}$ |
| A. | 0.2m<0.2n | B. | log0.3m>log0.3n | C. | 2m<2n | D. | m2>n2 |
| A. | 若m∥α,m∥n,则n∥α | B. | 若m⊥α,m∥n,则n⊥α | C. | 若m∥α,n?α,则m∥n | D. | 若m⊥n,n?α,则m⊥α |



