题目内容
13.某省高考实行“3+2”模式,“3”即语文、数学、外语为必考科目,“2”即考生从物理、化学、生物、政治、历史、地理六门学科中任选两门作为自己的考试科目,假定考生选择考试科目是等可能的,某考生在理、化中仅选一门作为考试科目的概率为$\frac{8}{15}$.分析 先求出基本事件总数,再求出某考生在理、化中仅选一门作为考试科目,包含的基本事件个数,由此能求出某考生在理、化中仅选一门作为考试科目的概率.
解答 解:∵考生从物理、化学、生物、政治、历史、地理六门学科中任选两门作为自己的考试科目,
假定考生选择考试科目是等可能的,
∴基本事件总数为n=${C}_{6}^{2}$=15,
某考生在理、化中仅选一门作为考试科目,包含的基本事件有以下8种情况:
{物理,生物},{物理,政治},{物理,历史},{物理,地理},{化学,生物},{化学,政治},{化学,历史},{化学,地理},
∴某考生在理、化中仅选一门作为考试科目的概率为p=$\frac{8}{15}$.
故答案为:$\frac{8}{15}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
18.下列说法中不正确的是( )
| A. | 对于定义域上的单调函数y=f(x),方程f(x)=a至多有一解 | |
| B. | 对于定义在(1,4)上的单调函数一定没有最大值,也没有最小值 | |
| C. | 如果存在a使得方程f(x)=a有两不同解,则函数y=f(x)必是非单调函数 | |
| D. | 定义在R上的单调函数,值域也是R |
8.已知函数f(x)是定义在区间(0,+∞)的可导函数,其导函数为f′(x),且满足xf′(x)>3f(x),则不等式8f(x)>f(2)x3的解集为( )
| A. | {x|x>3} | B. | {x|x>0} | C. | {x|x>2} | D. | {x|0<x>2} |
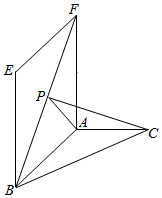 如图所示,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2$\sqrt{3}$,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一点,PF=3.
如图所示,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2$\sqrt{3}$,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一点,PF=3.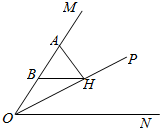 如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.