题目内容
2.函数f(x)=2x2-mx+3在(-∞,2)上是减函数,在(2,+∞)上是增函数,则m的值为8.分析 根据二次函数的性质,得到x=$\frac{m}{4}$=2,解出即可.
解答 解:由题意得:
对称轴x=$\frac{m}{4}$=2,
解得:m=8,
故答案为:8
点评 本题考查了二次函数的性质,考查了函数的单调性,是一道基础题.

练习册系列答案
相关题目
13.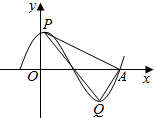 函数y=$\sqrt{3}$sin(ωx+φ)(ω>0,φ>0)的部分图象如图所示,设P,Q分别是图象的相邻的最高点和最低点,A是图象与x轴的交点,若AP⊥AQ,则ω的值为( )
函数y=$\sqrt{3}$sin(ωx+φ)(ω>0,φ>0)的部分图象如图所示,设P,Q分别是图象的相邻的最高点和最低点,A是图象与x轴的交点,若AP⊥AQ,则ω的值为( )
 函数y=$\sqrt{3}$sin(ωx+φ)(ω>0,φ>0)的部分图象如图所示,设P,Q分别是图象的相邻的最高点和最低点,A是图象与x轴的交点,若AP⊥AQ,则ω的值为( )
函数y=$\sqrt{3}$sin(ωx+φ)(ω>0,φ>0)的部分图象如图所示,设P,Q分别是图象的相邻的最高点和最低点,A是图象与x轴的交点,若AP⊥AQ,则ω的值为( )| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
10.已知a+a-1=2,则a-a-1的值为( )
| A. | 0 | B. | 2 | C. | -2 | D. | $\sqrt{2}$ |
7.解集{x|x≤1}用区间表示为( )
| A. | [-∞,1] | B. | (-∞,1] | C. | [1,+∞) | D. | [1,+∞] |
14.设a、b、c均为正实数,且3a=4b=6c,那么( )
| A. | $\frac{2}{c}=\frac{2}{a}+\frac{1}{b}$ | B. | $\frac{1}{c}=\frac{2}{a}+\frac{2}{b}$ | C. | $\frac{1}{c}=\frac{1}{a}+\frac{1}{b}$ | D. | $\frac{2}{c}=\frac{1}{a}+\frac{2}{b}$ |
16.设等差数列{an}的前n项和为Sn,已知S3=5,S6=15,则S9=( )
| A. | 35 | B. | 30 | C. | 25 | D. | 15 |
 如图,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
如图,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.