题目内容
8．A，B，C是不共线的三点，对空间任意一点O，有$\overrightarrow{OD}$=$\frac{1}{3}$（$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$）．则D点（ ）| A． | 不在平面ABC内 | B． | D是△ABC的重心 | C． | D是△ABC的外心 | D． | D是△ABC的垂心 |
分析 化简可得$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$；从而可得$\overrightarrow{AD}$=$\frac{2}{3}$（$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$））；从而确定答案．
解答 解：∵$\overrightarrow{OD}$=$\frac{1}{3}$（$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$），
∴$\overrightarrow{OD}$=$\overrightarrow{OA}$+$\frac{1}{3}$（$\overrightarrow{OB}$-$\overrightarrow{OA}$）+$\frac{1}{3}$（$\overrightarrow{OC}$-$\overrightarrow{OA}$），
∴$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$；
∴$\overrightarrow{AD}$=$\frac{2}{3}$（$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$））；
∴D是△ABC的重心；
故选：B．
点评 本题考查了向量的三角形法则与平行四边形法则的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．若圆x2+y2+2x+2y+1=0的面积被直线ax+by+1=0（a＞0，b＞0）平分．则ab的最大值是（ ）
| A． | $\frac{1}{16}$ | B． | $\frac{1}{4}$ | C． | 4 | D． | 16 |
13．
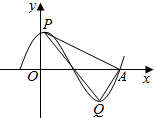函数y=$\sqrt{3}$sin（ωx+φ）（ω＞0，φ＞0）的部分图象如图所示，设P，Q分别是图象的相邻的最高点和最低点，A是图象与x轴的交点，若AP⊥AQ，则ω的值为（ ）
函数y=$\sqrt{3}$sin（ωx+φ）（ω＞0，φ＞0）的部分图象如图所示，设P，Q分别是图象的相邻的最高点和最低点，A是图象与x轴的交点，若AP⊥AQ，则ω的值为（ ）| A． | π | B． | $\frac{π}{2}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{4}$ |