题目内容
12.已知函数f(x)=$\frac{asinx+3(x+2)^{2}}{{x}^{2}+4}$(a是不为0的常数),当x∈[-2,2]时,函数f(x)的最大值与最小值的和为( )| A. | a+3 | B. | 6 | C. | 2 | D. | 3-a |
分析 根据函数f(x)的解析式,利用奇函数的单调性欲对称性,即可求出x∈[-2,2]时函数f(x)的最大值与最小值的和.
解答 解:函数f(x)=$\frac{asinx+3(x+2)^{2}}{{x}^{2}+4}$=$\frac{asinx}{{x}^{2}+4}$+$\frac{12x}{{x}^{2}+4}$+3,
设g(x)=$\frac{asinx}{{x}^{2}+4}$+$\frac{12x}{{x}^{2}+4}$,
则g(x)在x∈[-2,2]上是奇函数,且为单调函数,
所以g(-2)+g(2)=0;
当x∈[-2,2]时,函数f(x)的最大值与最小值的和为
f(2)+f(-2)=[g(2)+3]+[g(-2)+3]=6.
故选:B.
点评 本题考查了利用函数奇偶性与单调性求函数最大值与最小值和的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.不等式x(x-5)2>3(x-5)2的解集是( )
| A. | {x|x<-3} | B. | {x|3<x<5或x>5} | C. | {x|x>5} | D. | {x|3<x<5} |
3.已知抛物线C:y2=4x的焦点为F,点E(x0,y0)(y0>0)在C的准线l上,且线段EF的垂直平分线与抛物线C及直线l分别交于P、Q两点,若点Q的纵坐标为$\frac{3}{2}$,则P点的纵坐标为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
17.在△ABC中,A=60°,a2=bc,则△ABC一定是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
4.已知定义在R上的函数y=f(x)的导函数为f′(x),且满足f′(x)<f(x),f(0)=1,则不等式$\frac{f(x)}{{e}^{x}}$<1的解集为( )
| A. | (-∞,e4) | B. | (e4,+∞) | C. | (-∞,0) | D. | (0,+∞) |
1.甲同学练习投篮,每次投篮命中的概率为$\frac{1}{3}$,如果甲投篮3次,则甲至多有1次投篮命中的概率为( )
| A. | $\frac{20}{27}$ | B. | $\frac{4}{9}$ | C. | $\frac{8}{27}$ | D. | $\frac{1}{27}$ |
2.某人体检,依次要进行5项检查,其中甲项目不能排在最先,乙项目不能排在最后,则不同的检查顺序种数为( )
| A. | 38 | B. | 54 | C. | 78 | D. | 144 |
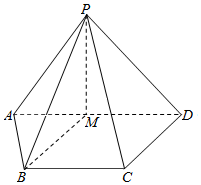 如图,在四棱锥P-ABCD中,AD∥BC,且AD=2BC,AD⊥CD,PA=PD,M为棱AD的中点.
如图,在四棱锥P-ABCD中,AD∥BC,且AD=2BC,AD⊥CD,PA=PD,M为棱AD的中点.