题目内容
4.已知定义在R上的函数y=f(x)的导函数为f′(x),且满足f′(x)<f(x),f(0)=1,则不等式$\frac{f(x)}{{e}^{x}}$<1的解集为( )| A. | (-∞,e4) | B. | (e4,+∞) | C. | (-∞,0) | D. | (0,+∞) |
分析 构造函数g(x)=$\frac{f(x)}{{e}^{x}}$(x∈R),研究g(x)的单调性,结合原函数的性质和函数值,即可求解.
解答 解:设g(x)=$\frac{f(x)}{{e}^{x}}$(x∈R),
则g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$,
∵f′(x)<f(x),
∴f′(x)-f(x)<0
∴g′(x)<0,
∴y=g(x)在定义域上单调递减
∵$\frac{f(x)}{{e}^{x}}$<1
∴g(x)<1
又∵g(0)=$\frac{f(0)}{{e}^{0}}$=1
∴g(x)<g(0)
∴x>0
故选:D.
点评 本题考查函数单调性与奇偶性的结合,结合已知条件构造函数,然后用导数判断函数的单调性是解题的关键.

练习册系列答案
相关题目
14.在如图所示的流程图中,若输入a,b,c的值分别为2,4,5,则输出的x=( )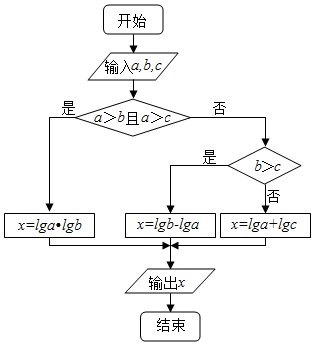

| A. | 1 | B. | 2 | C. | lg2 | D. | 10 |
15.“函数f(x)=kx-3在[-1,1]上有零点”是“k≥3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
12.已知函数f(x)=$\frac{asinx+3(x+2)^{2}}{{x}^{2}+4}$(a是不为0的常数),当x∈[-2,2]时,函数f(x)的最大值与最小值的和为( )
| A. | a+3 | B. | 6 | C. | 2 | D. | 3-a |
13.执行如图所示程序框图,则输出的n为( )


| A. | 3 | B. | 4 | C. | 6 | D. | 8 |