题目内容
3.已知抛物线C:y2=4x的焦点为F,点E(x0,y0)(y0>0)在C的准线l上,且线段EF的垂直平分线与抛物线C及直线l分别交于P、Q两点,若点Q的纵坐标为$\frac{3}{2}$,则P点的纵坐标为( )| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
分析 由抛物线方程求出焦点坐标,设出E的坐标(-1,m),利用EF和QP垂直求得m的值,可得G的坐标,求出QG所在直线方程,与抛物线C:y2=4x联立,求出P的坐标,即可求出P点的纵坐标.
解答 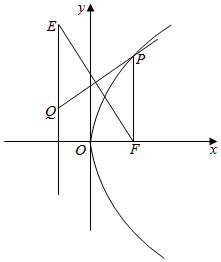 解:如图,由抛物线方程为y2=4x,得F(1,0),设E(-1,m)(m>0),
解:如图,由抛物线方程为y2=4x,得F(1,0),设E(-1,m)(m>0),
则EF中点为G(0,$\frac{m}{2}$),kEF=$\frac{m}{2}$,
又Q(-1,$\frac{3}{2}$),
∴kQG=$\frac{m-3}{2}$,则-$\frac{m}{2}$•$\frac{m-3}{2}$=-1,解得:m=4.
∴G(0,2),
∴QG所在直线方程为y-$\frac{3}{2}$=$\frac{1}{2}$(x+1),即x-2y+4=0.
联立$\left\{\begin{array}{l}{x-2y+4=0}\\{{y}^{2}=4x}\end{array}\right.$,得$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,即P(4,4),
故选:D.
点评 本题考查了抛物线的简单性质,考查了抛物线的应用,平面解析式的基础知识.考查了考生的基础知识的综合运用和知识迁移的能力,是中档题.

练习册系列答案
相关题目
14.在如图所示的流程图中,若输入a,b,c的值分别为2,4,5,则输出的x=( )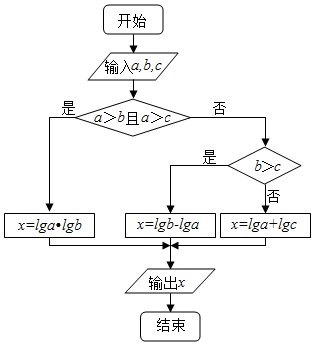

| A. | 1 | B. | 2 | C. | lg2 | D. | 10 |
11.设p:|x|<3,q:-1<x<3,则p是q成立的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 不充分不必要条件 |
18.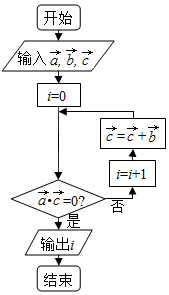 已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
 已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )
已知$\overrightarrow{a}$=$\overrightarrow{c}$=(-3,3),$\overrightarrow{b}$=(1,0),执行如图所示的程序框图,则输出i的值为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
8.如图,当输出的结果为36时,则该程序输入的是( )


| A. | 9 | B. | 3 | C. | 18 | D. | 6 |
15.“函数f(x)=kx-3在[-1,1]上有零点”是“k≥3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
12.已知函数f(x)=$\frac{asinx+3(x+2)^{2}}{{x}^{2}+4}$(a是不为0的常数),当x∈[-2,2]时,函数f(x)的最大值与最小值的和为( )
| A. | a+3 | B. | 6 | C. | 2 | D. | 3-a |
13.执行如图所示程序框图,则输出的n为( )


| A. | 3 | B. | 4 | C. | 6 | D. | 8 |