题目内容
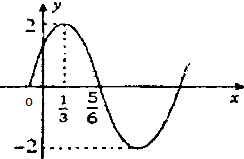
己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,则f(
)等于( )
| π |
| 2 |
| 3 |
| 2 |

A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由图象可得A=2,T=2,继而可得ω,由π•
+φ=2kπ+
(k∈Z)可求得φ,于是可得f(x)=2sin(πx+
),从而可求f(
)的值.
| 1 |
| 3 |
| π |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
解答:
解:由函数的图象可得A=2,
T=
=4(
-
)=2,解得ω=π;
∴f(x)=2sin(πx+φ),
又π•
+φ=2kπ+
(k∈Z),
∴φ=2kπ+
(k∈Z),而|φ|<
,
∴φ=
,
∴f(x)=2sin(πx+
),
∴f(
)=2sin(
+
)=-2cos
=-
,
故选:A.
T=
| 2π |
| ω |
| 5 |
| 6 |
| 1 |
| 3 |
∴f(x)=2sin(πx+φ),
又π•
| 1 |
| 3 |
| π |
| 2 |
∴φ=2kπ+
| π |
| 6 |
| π |
| 2 |
∴φ=
| π |
| 6 |
∴f(x)=2sin(πx+
| π |
| 6 |
∴f(
| 3 |
| 2 |
| 3π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 3 |
故选:A.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得f(x)=2sin(πx+
)是关键,属于中档题.
| π |
| 6 |

练习册系列答案
相关题目
若矩阵
满足下列条件:①每行中的四个数所构成的集合均为{1,2,3,4};②四列中至少有两列的上下两数是相同的.则这样的不同矩阵的个数为( )
|
| A、48 | B、72 |
| C、168 | D、312 |
已知数列{an}为等比数列,若a2,a8是方程2x2-7x+6=0的两个根,则a3•a5•a7的值是( )
| A、9 | ||
B、3
| ||
C、±3
| ||
| D、3 |
已知函数y=ax是R上的减函数,则函数y=loga(6+5x-x2)的单调增区间为( )
| A、(-∞,-1) | ||
B、(-1,
| ||
C、(
| ||
D、(
|
log21=( )
| A、2 | B、1 | C、0 | D、-1 |
轴截面为正三角形的圆锥称为等边圆锥,则等边圆锥的侧面积是底面积的( )倍.
| A、4 | ||
| B、3 | ||
| C、2 | ||
D、
|