题目内容
已知数列{an}为等比数列，若a2，a8是方程2x2-7x+6=0的两个根，则a3•a5•a7的值是（ ）
| A、9 | ||
B、3
| ||
C、±3
| ||
| D、3 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：由一元二次方程根与系数的关系可得a2 •a8 =3．再由等比数列的定义和性质可得a2 •a8 =3=a52，故a5=±
．从而求得a3•a5•a7的值．
| 3 |
解答：
解：∵数列{an}为等比数列，若a2，a8是方程2x2-7x+6=0的两个根，
∴a2 •a8 =3．
再由等比数列的定义和性质可得a2 •a8 =3=a52，故a5=±
．
故a3•a5•a7=±3
，
故选C．
∴a2 •a8 =3．
再由等比数列的定义和性质可得a2 •a8 =3=a52，故a5=±
| 3 |
故a3•a5•a7=±3
| 3 |
故选C．
点评：本题主要考查等比数列的定义和性质，一元二次方程根与系数的关系，属于中档题．
练习册系列答案
相关题目
函数f（x）=|tanx|•cosx的部分图象为（ ）
A、 |
B、 |
C、 |
D、 |
圆p：x2+y2=5，则经过点M（-1，2）的切线方程为（ ）
| A、x-2y-5=0 |
| B、x+2y+5=0 |
| C、x+2y-5=0 |
| D、x-2y+5=0 |
在△ABC中，已知a•tanB=b•tanA，则△ABC一定为（ ）
| A、等腰三角形 |
| B、Rt△ |
| C、等边三角形 |
| D、非直角的等腰三角形 |
对于有意实数x，符合[x]表示不超过x的最大整数，例如：[2]=2，[2.1]=2，已知数列{an}的通项公式是an=[log2（2n-1）]，设数列{an}的前n项和为Sn，若Sn=2013，则n等于（ ）
| A、426 | B、425 |
| C、424 | D、423 |
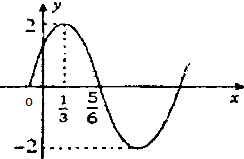
己知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）的部分图象如图所示，则f（
）等于（ ）
| π |
| 2 |
| 3 |
| 2 |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
已知函数f（x）=|log
x|的定义域为[a，b]，值域为[0，2]，则|b-a|的最小值为（ ）
| 1 |
| 2 |
A、
| ||
| B、3 | ||
| C、4 | ||
D、
|