题目内容
轴截面为正三角形的圆锥称为等边圆锥，则等边圆锥的侧面积是底面积的（ ）倍．
| A、4 | ||
| B、3 | ||
| C、2 | ||
D、
|
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：由题意，求出圆锥的底面面积，侧面面积，即可得到比值．
解答：
解：圆锥的轴截面是正三角形，设底面半径为r，则它的底面积为πr2；
圆锥的侧面积为：
×2rπ•2r=2πr2；
圆锥的侧面积是底面积的2倍．
故选：C
圆锥的侧面积为：
| 1 |
| 2 |
圆锥的侧面积是底面积的2倍．
故选：C
点评：本题是基础题，考查圆锥的特征，底面面积，侧面积的求法，考查计算能力，是送分题．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=|tanx|•cosx的部分图象为（ ）
A、 |
B、 |
C、 |
D、 |
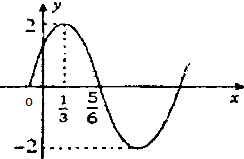
己知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）的部分图象如图所示，则f（
）等于（ ）
| π |
| 2 |
| 3 |
| 2 |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
已知函数f（x）=|log
x|的定义域为[a，b]，值域为[0，2]，则|b-a|的最小值为（ ）
| 1 |
| 2 |
A、
| ||
| B、3 | ||
| C、4 | ||
D、
|
函数y=2x3-2x2在[-1，2]上的最大值，最小值为（ ）
| A、0、-3 | B、8、-3 |
| C、10、8 | D、8、-4 |
平面上有n个圆，其中每两个圆都相交于两点，每三个圆不共点，这几个圆将平面最多分成f（n）个部分，则f（n）的表达式为（ ）
| A、2n |
| B、n2-n+2 |
| C、2n-（n-1）（n-2）（n-3） |
| D、n3-5n2+10n-4 |
要得到函数y=2x+1-2的图象，可将函数y=2x的图象（ ）
| A、向左平移1个单位，再向上平移2个单位 |
| B、向左平移1个单位，再向下平移2个单位 |
| C、向右平移1个单位，再向上平移2个单位 |
| D、向右平移1个单位，再向下平移2个单位 |
如图，四棱锥P-ABCD的底面ABCD是矩形，侧面PAB是正三角形，AB=2，BC=