题目内容
设函数f（x）=ax3+bx+c（a≠0）为奇函数，其图象在点（1，f（1））处的切线与直线x-6y-7=0垂直，导函数f′（x）的最小值为-12．求函数f（x）的解析式．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用,导数的综合应用
分析：根据函数f（x）为奇函数，得出c=0．这时，f′（x）=3ax2+b，由f′（x）最小值为-12，得出b=-12．而通过切线与直线x-6y-7=0垂直，求出切线斜率为-6，根据函数在切点处的导数与切线斜率的关系能求出a，从而求出f（x）解析式．
解答：
解：∵f（x）为奇函数；
∴c=0；
∴f（x）=ax3+bx，f′（x）=3ax2+b；
∴b=-12，（3a-12）•
=-1；
∴a=2
∴f（x）=2x3-12x．
∴c=0；
∴f（x）=ax3+bx，f′（x）=3ax2+b；
∴b=-12，（3a-12）•
| 1 |
| 6 |
∴a=2
∴f（x）=2x3-12x．
点评：考查奇函数的概念，二次函数的最值，以及函数在切点处的导数与切线斜率的关系，相互垂直的两直线斜率的关系．
练习册系列答案
相关题目
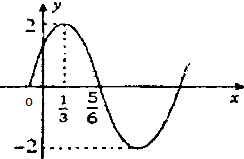
己知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）的部分图象如图所示，则f（
）等于（ ）
| π |
| 2 |
| 3 |
| 2 |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
要得到函数y=2x+1-2的图象，可将函数y=2x的图象（ ）
| A、向左平移1个单位，再向上平移2个单位 |
| B、向左平移1个单位，再向下平移2个单位 |
| C、向右平移1个单位，再向上平移2个单位 |
| D、向右平移1个单位，再向下平移2个单位 |
如图，直三棱柱ABC-A1B1C1中，已知∠ACB=90°，AC=BC=1，BB1=2，M，N分别是B1C1和AB的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，侧面PAB是正三角形，AB=2，BC=