题目内容
设函数f(x)=ax3-3x+1(x∈R),若对于任意x∈[-1,1],都有f(x)≥0成立,则实数a的值为( )
| A、0 | B、2 | C、4 | D、1 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:首先由f(x)=ax3-3x+1,可得f′(x)=3ax2-3,(1)当a≤0时,3ax2-3<0,函数f(x)是减函数,f(x)min=f(1)=a-2≥0,解得a≥2,与已知矛盾;(2)当a>0时,令f′(x)=0,可得x=±
,根据对于任意x∈[-1,1],都有f(x)≥0成立,分类讨论,求出a的取值范围即可.
| ||
| a |
解答:
解:由f(x)=ax3-3x+1,
可得f′(x)=3ax2-3,
(1)当a≤0时,3ax2-3<0,
函数f(x)是减函数,
f(x)min=f(1)=a-2≥0,
解得a≥2,与已知矛盾;
(2)当a>0时,令f′(x)=0,可得x=±
,
①当x<-
时,f′(x)>0,f(x)为递增函数,
②当-
<x<
时,f′(x)<0,f(x)为递减函数,
③当x>
时,f(x)为递增函数;
所以f(
)≥0,f(-1)≥0,且f(1)≥0,
由f(
)≥0,解得a≥4,
由f(-1)≥0,解得a≤4,
由f(1)≥0解得2≤a≤4,
综上,可得a=4.
故选:C.
可得f′(x)=3ax2-3,
(1)当a≤0时,3ax2-3<0,
函数f(x)是减函数,
f(x)min=f(1)=a-2≥0,
解得a≥2,与已知矛盾;
(2)当a>0时,令f′(x)=0,可得x=±
| ||
| a |
①当x<-
| ||
| a |
②当-
| ||
| a |
| ||
| a |
③当x>
| ||
| a |
所以f(
| ||
| a |
由f(
| ||
| a |
由f(-1)≥0,解得a≤4,
由f(1)≥0解得2≤a≤4,
综上,可得a=4.
故选:C.
点评:此题主要考查了利用导数求闭区间上函数的最值问题,考查了分类讨论思想的应用,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
圆p:x2+y2=5,则经过点M(-1,2)的切线方程为( )
| A、x-2y-5=0 |
| B、x+2y+5=0 |
| C、x+2y-5=0 |
| D、x-2y+5=0 |
对于有意实数x,符合[x]表示不超过x的最大整数,例如:[2]=2,[2.1]=2,已知数列{an}的通项公式是an=[log2(2n-1)],设数列{an}的前n项和为Sn,若Sn=2013,则n等于( )
| A、426 | B、425 |
| C、424 | D、423 |
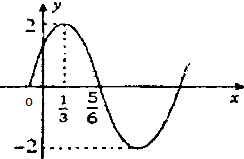
己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,则f(
)等于( )
| π |
| 2 |
| 3 |
| 2 |

A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
设x,y∈R,则xy<0是|x-y|=|x|+|y|成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分且必要条件 |
| D、既不充分又不必要条件 |
已知函数f(x)=|log
x|的定义域为[a,b],值域为[0,2],则|b-a|的最小值为( )
| 1 |
| 2 |
A、
| ||
| B、3 | ||
| C、4 | ||
D、
|
平面上有n个圆,其中每两个圆都相交于两点,每三个圆不共点,这几个圆将平面最多分成f(n)个部分,则f(n)的表达式为( )
| A、2n |
| B、n2-n+2 |
| C、2n-(n-1)(n-2)(n-3) |
| D、n3-5n2+10n-4 |