题目内容
已知函数y=ax是R上的减函数,则函数y=loga(6+5x-x2)的单调增区间为( )
| A、(-∞,-1) | ||
B、(-1,
| ||
C、(
| ||
D、(
|
考点:复合函数的单调性
专题:函数的性质及应用
分析:由题意可得0<a<1,令t=6+5x-x2 >0,求得函数y=loga(6+5x-x2)的定义域,且y=logat,本题即求函数t在定义域内的减区间.再结合二次函数的性质可得t=-(x-
)2+
在定义域内的减区间.
| 5 |
| 2 |
| 49 |
| 4 |
解答:
解:∵函数y=ax是R上的减函数,∴0<a<1.
令t=6+5x-x2 >0,求得-1<x<6,则函数y=loga(6+5x-x2)的定义域为(-1,6),且y=logat.
则函数y=loga(6+5x-x2)的单调增区间,即函数t在定义域内的减区间.
结合二次函数的性质可得t=-(x-
)2+
在定义域内的减区间为(
,6),
故选:C.
令t=6+5x-x2 >0,求得-1<x<6,则函数y=loga(6+5x-x2)的定义域为(-1,6),且y=logat.
则函数y=loga(6+5x-x2)的单调增区间,即函数t在定义域内的减区间.
结合二次函数的性质可得t=-(x-
| 5 |
| 2 |
| 49 |
| 4 |
| 5 |
| 2 |
故选:C.
点评:本题主要考查复合函数的单调性,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
若角α的终边经过点P(1,-2),则tan2α的值为( )
A、
| ||
B、
| ||
C、
| ||
D、-
|
在△ABC中,已知a•tanB=b•tanA,则△ABC一定为( )
| A、等腰三角形 |
| B、Rt△ |
| C、等边三角形 |
| D、非直角的等腰三角形 |
已知
+2
+22
+…+2n
=729,则
+
+
的值等于( )
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 1 n |
| C | 3 n |
| C | 5 n |
| A、64 | B、32 | C、63 | D、31 |
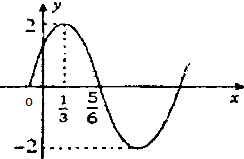
己知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,则f(
)等于( )
| π |
| 2 |
| 3 |
| 2 |

A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
设m∈R,则关于x的方程x2+4x+2=m有解的一个必要不充分条件是( )
| A、m>-2 | B、m<-2 |
| C、m>-3 | D、m<-3 |
函数y=2x3-2x2在[-1,2]上的最大值,最小值为( )
| A、0、-3 | B、8、-3 |
| C、10、8 | D、8、-4 |
 如图,直三棱柱ABC-A1B1C1中,已知∠ACB=90°,AC=BC=1,BB1=2,M,N分别是B1C1和AB的中点.
如图,直三棱柱ABC-A1B1C1中,已知∠ACB=90°,AC=BC=1,BB1=2,M,N分别是B1C1和AB的中点.