题目内容
将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体.经过搅拌后,从中随机取出一个小正方体,记它的涂油漆面数为X,则P(X≥2)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:由题意可知:此题为古典概型,基本事件总数为125个.其中“X≥2”包含以下两类:
①8个顶点处的8个小正方体涂有3面,
②每一条棱上除了两个顶点处的小正方体,还剩下3个,一共有3×12=36个小正方体涂有2面,
根据古典概型的计算公式即可得出.
①8个顶点处的8个小正方体涂有3面,
②每一条棱上除了两个顶点处的小正方体,还剩下3个,一共有3×12=36个小正方体涂有2面,
根据古典概型的计算公式即可得出.
解答:
解:由题意可知:基本事件中数为125个,X所有可能取值为0,1,2,3,
①8个顶点处的8个小正方体涂有3面,∴P(X=3)=
;
②每一条棱上除了两个顶点处的小正方体,还剩下3个,一共有3×12=36个小正方体涂有2面,∴P(X=2)=
;
故P(X≥2)=
=
故选:A.
①8个顶点处的8个小正方体涂有3面,∴P(X=3)=
| 8 |
| 125 |
②每一条棱上除了两个顶点处的小正方体,还剩下3个,一共有3×12=36个小正方体涂有2面,∴P(X=2)=
| 36 |
| 125 |
故P(X≥2)=
| 8+36 |
| 125 |
| 44 |
| 125 |
故选:A.
点评:正确找出所涂油漆的面数的正方体的个数及古典概型的概率计算公式是解题的关键.

练习册系列答案
相关题目
已知四棱锥P-ABCD的三视图如图所示,则此四棱锥的四个侧面的面积中最大的是( )


| A、3 | ||||
B、
| ||||
C、3
| ||||
D、
|
按如图所示程序框,最后输出i的结果是( )

| A、5 | B、6 | C、7 | D、8 |
已知集合A={x|5-|2x-3|∈N*},则集合A的非空真子集数为( )
| A、14 | B、512 |
| C、511 | D、510 |
已知偶函数f(x)的定义域为R,对任意x∈R,有f(x+2)=f(x),当x∈[0,1]时,f(x)=-x+1.则函数g(x)=log6|x|-f(x)的零点的个数是( )
| A、6个 | B、8个 |
| C、10个 | D、12个 |
若集合S满足对任意的a,b∈S,有a±b∈S,则称集合S为“闭集”,下列集合中不是“闭集”的是( )
| A、自然数集N | B、整数集Z |
| C、有理数集Q | D、实数集R |
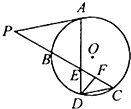 如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=
如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=