题目内容
已知定义在R上的可导函数f(x)满足:f′(x)+f(x)<0,则
与f(1)(e是自然对数的底数)的大小关系是( )
| f(m-m2) |
| em2-m+1 |
A、
| ||
B、
| ||
C、
| ||
| D、不确定 |
考点:导数的运算
专题:导数的概念及应用
分析:构造函数g(x)=exf(x),利用导数研究其单调性,注意到已知f′(x)+f(x)<0,可得g(x)为单调减函数,最后由m-m2=-(m-
)2+
<1,代入函数解析式即可得答案.
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:设g(x)=exf(x),
∵f′(x)+f(x)<0,
∴g′(x)=ex(f′(x)+f(x))<0
∴函数g(x)为R上的减函数;
∵m-m2=-(m-
)2+
<1,∴g(m-m2)>g(1)
即em-m2f(em-m2)>e1f(1),
∴
>f(1)
故选:A.
∵f′(x)+f(x)<0,
∴g′(x)=ex(f′(x)+f(x))<0
∴函数g(x)为R上的减函数;
∵m-m2=-(m-
| 1 |
| 2 |
| 1 |
| 4 |
即em-m2f(em-m2)>e1f(1),
∴
| f(m-m2) |
| em2-m+1 |
故选:A.
点评:本题考查了利用导数研究函数的单调性,恰当的构造函数,并能利用导数研究其性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知偶函数f(x)的定义域为R,对任意x∈R,有f(x+2)=f(x),当x∈[0,1]时,f(x)=-x+1.则函数g(x)=log6|x|-f(x)的零点的个数是( )
| A、6个 | B、8个 |
| C、10个 | D、12个 |
若向量
=(6,x)(x∈R)则“x=8”是“|
|=10”的( )
| a |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知复数z=x+yi(x,y∈R),且z2=8i(i是虚数单位),则z=( )
| A、2+2i |
| B、-2+2i或-2-2i |
| C、-2-2i |
| D、2+2i或-2-2i |
已知圆F的圆心为双曲线
-
=1的右焦点,且与该双曲线的渐近线相切,则圆F的方程为( )
| x2 |
| 5 |
| y2 |
| 4 |
| A、(x+3)2+y2=4 |
| B、(x+3)2+y2=2 |
| C、(x-3)2+y2=4 |
| D、(x-3)2+y2=2 |
若集合S满足对任意的a,b∈S,有a±b∈S,则称集合S为“闭集”,下列集合中不是“闭集”的是( )
| A、自然数集N | B、整数集Z |
| C、有理数集Q | D、实数集R |
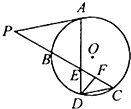 如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=
如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=