题目内容
祖暅原理对平面图形也成立,即夹在两条平行线间的两个平面图形被任意一条平行于这两条直线的直线截得的线段总相等,则这两个平面图形面积相等.利用这个结论解答问题:函数f(x)=2x、g(x)=2x-1与直线x=0,x=1所围成的图形的面积为 .
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:由题意可知,函数f(x),g(x)与x=0,直线x=1围成的图形的面积是:∫012x-(2x-1)dx,然后根据积分的运算公式进行求解即可.
解答:
解:由于f(x)=2x、g(x)=2x-1与直线x=0,x=1所围成的图形的面积是:
∫012x-(2x-1)dx=(x)|01=1,
则曲线围成的图形的面积为1,
故答案为:1.
∫012x-(2x-1)dx=(x)|01=1,
则曲线围成的图形的面积为1,
故答案为:1.
点评:本题考查函数的图象,定积分,考查计算能力,解题的关键是两块封闭图形的面积之和就是上部直接积分减去下部积分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知四棱锥P-ABCD的三视图如图所示,则此四棱锥的四个侧面的面积中最大的是( )


| A、3 | ||||
B、
| ||||
C、3
| ||||
D、
|
已知集合A={x|5-|2x-3|∈N*},则集合A的非空真子集数为( )
| A、14 | B、512 |
| C、511 | D、510 |
已知复数z=x+yi(x,y∈R),且z2=8i(i是虚数单位),则z=( )
| A、2+2i |
| B、-2+2i或-2-2i |
| C、-2-2i |
| D、2+2i或-2-2i |
 阅读如图所示的程序框图,如果输入的n的值为6,那么运行相应程序,输出的n的值为
阅读如图所示的程序框图,如果输入的n的值为6,那么运行相应程序,输出的n的值为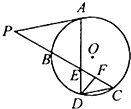 如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=
如图,A是⊙O上的点,PC与⊙O相交于B、C两点,点D在⊙O上,CD∥AP,AD与BC交于E,F为CE上的点,若∠EDF=∠P,BE=8,EF=4,FC=5,则PB=