题目内容
17.设{an}是公差不为0的等差数列,a1=2且a32=a1a6,则{an}的前n项和Sn=( )| A. | $\frac{{n}^{2}}{4}$+$\frac{7n}{4}$ | B. | $\frac{{n}^{2}}{3}$+$\frac{5n}{3}$ | C. | $\frac{{n}^{2}}{2}$+$\frac{3n}{4}$ | D. | n2+n |
分析 设公差为d,由a1=2且a32=a1a6,求出公差d=$\frac{1}{2}$,再根据等差数列的前n项公式计算即可.
解答 解:设公差为d,a1=2且a32=a1a6,
∴(2+2d)2=2(2+5d),
解得d=$\frac{1}{2}$,或d=0(舍去),
∴{an}的前n项和Sn=2n+$\frac{n(n-1)×\frac{1}{2}}{2}$=$\frac{{n}^{2}+7n}{4}$,
故选:A.
点评 本题考查了等差数列的通项公式和前n项公式,属于基础题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
8.已知向量$\overrightarrow{a}$=(1,2,1),$\overrightarrow{b}$=(x,-1,1),若$\overrightarrow{a}⊥\overrightarrow{b}$,则实数x的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
5.在等差数列中,连续四项为a,x,b,2x,那么a:b=( )
| A. | 1:4 | B. | 1:3 | C. | 1:3或1 | D. | 1:2 |
12.等比数列{an}中,a1、a8是方程x2+2x-5=0的两个根,则a4a5等于( )
| A. | -5 | B. | -2 | C. | 2 | D. | 5 |
2.复数z满足$\frac{z}{z-i}$=i(i为虚数单位),则$\overline{z}$=( )
| A. | 1+i | B. | 1-i | C. | $\frac{1+i}{2}$ | D. | $\frac{1-i}{2}$ |
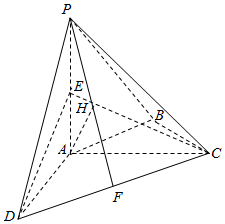 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BCA=45°,AP=AD=AC=2,E、F、H分别为PA、CD、PF的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BCA=45°,AP=AD=AC=2,E、F、H分别为PA、CD、PF的中点.