将边长为2的正方形ABCD沿对角线BD折成直二面角A-BD-C.则异面直线AB与CD所成的角60°．题目和参考答案——青夏教育精英家教网—

题目内容

14．将边长为2的正方形ABCD沿对角线BD折成直二面角A-BD-C，则异面直线AB与CD所成的角60°．

分析建立空间坐标系，利用向量法，求出AB与CD所成的角．

解答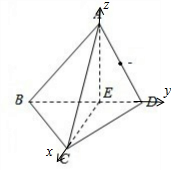解：以E为坐标原点，EC、ED、EA分别为x，y，z轴建立直角坐标系，?
则A（0，0，$\sqrt{2}$），B（0，-$\sqrt{2}$，0），D（0，$\sqrt{2}$，0），C（$\sqrt{2}$，0，0）．
$\overrightarrow{AB}$=（0，-$\sqrt{2}$，-$\sqrt{2}$），$\overrightarrow{DC}$=（$\sqrt{2}$，-$\sqrt{2}$，0）．
cos＜$\overrightarrow{AB}$，$\overrightarrow{DC}$＞=$\frac{1}{2}$，
∴＜$\overrightarrow{AB}$，$\overrightarrow{DC}$＞=60°，
故答案为：60°．

点评本题考查异面直线的夹角，考查向量方法的运用，属于中档题．

练习册系列答案

5．设△ABC三个内角A，B，C所对的边分别为a，b，c，若a²sinC=4sinA，（ca+cb）（sinA-sinB）=sinC（2$\sqrt{7}$-c²），则△ABC的面积为$\frac{3}{2}$．

2．

已知点$A（{2\sqrt{2}，2}）$在抛物线C：x²=2py（p＞0）上．
（1）求抛物线C的方程；
（2）设定点D（0，m），过D作直线y=kx+m（k＞0）与抛物线C交于M（x₁，y₁），N（x₂，y₂）（y₁＜y₂）两点，连接ON（O为坐标原点），过点M作垂直于x轴的直线交ON于点G．
①证明点G在一条定直线上；
②求四边形ODMG的面积的最大值．

9．

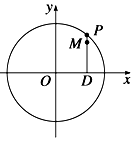如图，设P是圆x²+y²=6上的动点，点D是P在x轴上的投影，M为PD上一点，且$\overrightarrow{DP}=\sqrt{2}\overrightarrow{DM}$．
（1）当P在圆上运动时，求点M的轨迹C的方程；
（2）若点Q（1，1）恰为直线l与曲线C相交弦的中点，试确定直线l的方程；
（3）直线$x+y-\sqrt{3}=0$与曲线C相交于E、G两点，F、H为曲线C上两点，若四边形EFGH对角线相互垂直，求S_EFGH的最大值．

19．

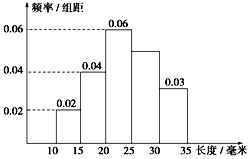对一批零件的长度（单位：mm）进行抽样检测，检测结果的频率分布直方图如图所示．根据标准，零件长度在区间[20，25）上的为一等品，在区间[15，20）和区间[25，30）上的为二等品，在区间[10，15）和[30，35）上的为三等品．
（Ⅰ）用频率估计概率，现从该批产品中随机抽取一件，求其为二等品的概率；
（Ⅱ）已知检测结果为一等品的有6件，现随机从三等品中取两件，求取出的两件产品中恰有1件的长度在区间[30，35）上的概率．

6．设有直线m，n和平面α，β，下列四个命题中，正确的是（　　）

	A．	若m∥α，n∥α，则m∥n		B．	若m?α，n?α，m∥β，l∥β，则α∥β
	C．	若α⊥β，m?α，则m⊥β		D．	若α⊥β，m⊥β，m?α，则m∥α

4．在△ABC中，三内角A、B、C对应的边分别为a、b、c，且a=1，$A=\frac{π}{6}$．
（Ⅰ）当$b=\sqrt{3}$，求角C的大小；
（Ⅱ）求△ABC面积最大值．

试题分类