题目内容
4.在△ABC中,三内角A、B、C对应的边分别为a、b、c,且a=1,$A=\frac{π}{6}$.(Ⅰ)当$b=\sqrt{3}$,求角C的大小;
(Ⅱ)求△ABC面积最大值.
分析 (Ⅰ)由已知及正弦定理可得sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}}{2}$,结合范围B∈(0,$\frac{5π}{6}$),可求B的值,进而可求C的值.
(Ⅱ)由已知及余弦定理,基本不等式可求1≥bc,进而利用三角形面积公式即可得解.
解答 解:(Ⅰ)∵a=1,A=$\frac{π}{6}$,b=$\sqrt{3}$,
∴由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}×\frac{1}{2}}{1}$=$\frac{\sqrt{3}}{2}$,
又∵B∈(0,$\frac{5π}{6}$),
∴B=$\frac{π}{3}$,或$\frac{2π}{3}$.
∴C=π-A-B=$\frac{π}{2}$,或$\frac{π}{6}$.
(Ⅱ)∵a=1,A=$\frac{π}{6}$.
∴由余弦定理可得:
a2=b2+c2-2bccosA
即1=b2+c2-$\sqrt{3}$bc≥2bc-$\sqrt{3}$bc=(2-$\sqrt{3}$)bc,
所以bc≤$\frac{1}{2-\sqrt{3}}$(当且仅当b=c=1时等号成立)
∴SABC=$\frac{1}{2}$bcsinA≤$\frac{1}{2}$×$\frac{1}{2-\sqrt{3}}$×$\frac{1}{2}$=$\frac{2+\sqrt{3}}{4}$,(当且仅当b=c=1时等号成立),即△ABC面积最大值$\frac{2+\sqrt{3}}{4}$.
点评 本题主要考查了正弦定理,余弦定理,基本不等式,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.对于给定的样本点所建立的模型A和模型B,它们的残差平方和分别是${a_1},{a_2},{R^2}$的值分别为b1,b2,下列说法正确的是( )
| A. | 若a1<a2,则b1<b2,A的拟合效果更好 | |
| B. | 若a1<a2,则b1<b2,B的拟合效果更好 | |
| C. | 若a1<a2,则b1>b2,A的拟合效果更好 | |
| D. | 若a1<a2,则b1>b2,B的拟合效果更好 |
16.在△ABC中,根据下列条件解三角形,其中有两解的是( )
| A. | b=7,c=3,C=30° | B. | a=20,b=30,C=30° | C. | b=4,c=2$\sqrt{3}$,C=60° | D. | b=5,c=4,C=45° |
13.P(3,y)为α终边上一点,$cosα=\frac{3}{5}$,则y=( )
| A. | -3 | B. | 4 | C. | ±3 | D. | ±4 |
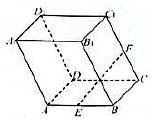 如图所示,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,侧棱AA1的长为2,且∠A1AB=∠A1AD=120°,E为AB的中点,F为CC1的中点,则EF的长为$\sqrt{3}$.
如图所示,在平行六面体ABCD-A1B1C1D1中,底面是边长为2的正方形,侧棱AA1的长为2,且∠A1AB=∠A1AD=120°,E为AB的中点,F为CC1的中点,则EF的长为$\sqrt{3}$.