题目内容
2. 已知点$A({2\sqrt{2},2})$在抛物线C:x2=2py(p>0)上.
已知点$A({2\sqrt{2},2})$在抛物线C:x2=2py(p>0)上.(1)求抛物线C的方程;
(2)设定点D(0,m),过D作直线y=kx+m(k>0)与抛物线C交于M(x1,y1),N(x2,y2)(y1<y2)两点,连接ON(O为坐标原点),过点M作垂直于x轴的直线交ON于点G.
①证明点G在一条定直线上;
②求四边形ODMG的面积的最大值.
分析 (1)根据抛物线的性质即可求出,
(2)①联立方程组,根据韦达定理可得yD=y=$\frac{{y}_{2}}{{x}_{2}}$x1=$\frac{\frac{1}{4}{{x}_{2}}^{2}}{{x}_{2}}$•x1=$\frac{{x}_{1}{x}_{2}}{4}$=-m为定值,
②易知四边形ODMG为梯形,求出面积的表达式,利用导数求出函数的最值即可.
解答 解:(1)∵A(2$\sqrt{2}$,2)在抛物线x2=2py上,
∴(2$\sqrt{2}$)2=4p,解得p=2,
∴抛物线的方程为:x2=4y,
(2)①由$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}=4y}\end{array}\right.$,消去y整理得x2-4kx-4m=0,
∵M(x1,y1),N(x2,y2)(y1<y2)是y=kx+m(k>0)与抛物线C的交点,
∴x1+x2=4k,x1x2=-4m,
∵直线ON的方程为:y=$\frac{{y}_{2}}{{x}_{2}}$x,
∴yD=y=$\frac{{y}_{2}}{{x}_{2}}$x1=$\frac{\frac{1}{4}{{x}_{2}}^{2}}{{x}_{2}}$•x1=$\frac{{x}_{1}{x}_{2}}{4}$=-m为定值,
∴点G在一条定直线y=-m上,
②易知四边形ODMG为梯形,
∴S=$\frac{1}{2}$[-m+(-m-y1)]x1=$\frac{1}{2}$(-2m-$\frac{{x}_{1}^{2}}{4}$)x1=mx1-$\frac{1}{8}{x}_{1}^{2}$,
结合图形可知0<x1<2$\sqrt{-m}$(x1=-$\sqrt{-\frac{8}{3}m}$舍去)
由S′=-m-$\frac{3}{8}{x}_{1}^{2}$,当S′=0时,
解得x1=$\sqrt{-\frac{8}{3}m}$<2$\sqrt{-m}$,(x1=-$\sqrt{-\frac{8}{3}m}$舍去),
当x1∈(0,$\sqrt{-\frac{8}{3}m}$)上单调递增,在($\sqrt{-\frac{8}{3}m}$,2$\sqrt{-m}$)单调递减,
∴当x1=$\sqrt{-\frac{8}{3}m}$时,Smax=-m$\sqrt{-\frac{8}{3}m}$-$\frac{1}{8}$(-$\frac{8}{3}$m•)$\sqrt{-\frac{8}{3}m}$=-$\frac{4m\sqrt{-6m}}{9}$
点评 本题考查了抛物线的性质以及韦达定理和导数再面积的应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $y=sin({\frac{x}{2}+\frac{5π}{6}})$ | B. | $y=sin({2x-\frac{π}{6}})$ | C. | y=2sin2x-1 | D. | $y=cos({2x-\frac{π}{6}})$ |
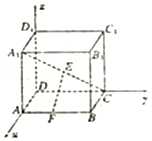 如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )
如图所示,在空间直角坐标系中,D是坐标原点,有一棱长为a的正方体ABCD-A1B1C1D1,E和F分别是体对角线A1C和棱AB上的动点,则|EF|的最小值为( )| A. | $\sqrt{2}a$ | B. | $\frac{{\sqrt{2}}}{2}a$ | C. | a | D. | $\frac{1}{2}a$ |
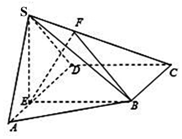 如图,在四棱锥S-ABCD中,平面SAD⊥底面ABCD,$∠SAD=\frac{π}{3}$,在AD边上取一点E,使得BCDE为矩形,SA=2AE=DE=2.
如图,在四棱锥S-ABCD中,平面SAD⊥底面ABCD,$∠SAD=\frac{π}{3}$,在AD边上取一点E,使得BCDE为矩形,SA=2AE=DE=2.