题目内容
已知lnx=2+ln(
),求x.
| 2 |
| x |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:直接利用对数的运算法则化简求解才即可.
解答:
解:由lnx=2+ln(
),可知x>0.
化简可得:lnx=ln(
e2),
∴x=
,
解得:x=
e.
| 2 |
| x |
化简可得:lnx=ln(
| 2 |
| x |
∴x=
| 2e2 |
| x |
解得:x=
| 2 |
点评:本题考查函数与方程的应用,考查计算能力.

练习册系列答案
相关题目
已知cos(θ+
)=-
,θ∈(0,
),则cos2θ=( )
| π |
| 4 |
| ||
| 10 |
| π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知集合A={x|y=
,B={y|y=
,则A∩B=( )
| 1-x |
| 1-x |
| A、{1} | B、R |
| C、{-∞,1} | D、[0.1] |
已知命题p:2<x<3,q:x2-5x+4<0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=2
,E为CC1的中点,则直线BE与AC1所成角的余弦值为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
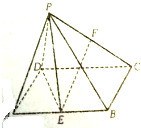 如图,在四棱锥P-ABCD中,底面为矩形ABCD,E,F分别为AB,PC的中点,且PD=PE,PB=PC,求证:
如图,在四棱锥P-ABCD中,底面为矩形ABCD,E,F分别为AB,PC的中点,且PD=PE,PB=PC,求证: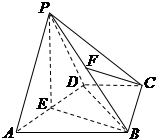 如图,在四棱锥P-ABCD中,侧面PAD是等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB的中点.
如图,在四棱锥P-ABCD中,侧面PAD是等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB的中点.