题目内容
已知集合{(x,y)|
}表示的平面区域为Ω,在区域Ω内任取一点P(x,y),若点P的坐标满足不等式y≤kx的概率为
,则k= .
|
| 2 |
| 3 |
考点:几何概型
专题:计算题,概率与统计
分析:由
,可得B(
,
),由
,可得A(4,-4),设直线y=kx与直线AB交于C,利用在区域Ω内任取一点P(x,y),点P的坐标满足不等式y≤kx的概率为
,可得2BC=CA,求出C的坐标,即可得到答案.
|
| 4 |
| 3 |
| 4 |
| 3 |
|
| 2 |
| 3 |
解答:
解:由
,可得B(
,
),
由
,可得A(4,-4),
设直线y=kx与直线AB交于C,则
∵在区域Ω内任取一点P(x,y),点P的坐标满足不等式y≤kx的概率为
,
∴2BC=CA,
∴C(
,-
),
∴k=-
.
故答案为:-
.
|
| 4 |
| 3 |
| 4 |
| 3 |
由
|
设直线y=kx与直线AB交于C,则
∵在区域Ω内任取一点P(x,y),点P的坐标满足不等式y≤kx的概率为
| 2 |
| 3 |
∴2BC=CA,
∴C(
| 20 |
| 9 |
| 4 |
| 9 |
∴k=-
| 1 |
| 5 |
故答案为:-
| 1 |
| 5 |
点评:本题考查的知识点是几何概型,二元一次不等式(组)与平面区域,求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=N(A)/N求解.

练习册系列答案
相关题目
已知集合A={x|y=
,B={y|y=
,则A∩B=( )
| 1-x |
| 1-x |
| A、{1} | B、R |
| C、{-∞,1} | D、[0.1] |
已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=2
,E为CC1的中点,则直线BE与AC1所成角的余弦值为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
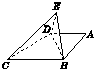 如图,在直角梯形ABCD中,AD∥BC,AD=AB,∠A=90°,BD⊥DC,将△ABD沿BD折起到△EBD的位置,使平面EBD⊥平面BDC.
如图,在直角梯形ABCD中,AD∥BC,AD=AB,∠A=90°,BD⊥DC,将△ABD沿BD折起到△EBD的位置,使平面EBD⊥平面BDC. 如图是输出4000以内的能被3和5整除的所有正整数的算法流程图,则在①处应填
如图是输出4000以内的能被3和5整除的所有正整数的算法流程图,则在①处应填



