题目内容
12．
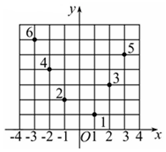如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横、纵坐标分别对应数列{an}（n∈N*）的前12项（即横坐标为奇数项，纵坐标为偶数项），按如此规律下去，则a2009+a2010+a2011等于（ ）| A． | 2 011 | B． | 1 006 | C． | 1 005 | D． | 1 003 |
分析 奇数项为1，-1，2，-2…，发现a2n-1+a2n+1=0，偶数项为1，2，3…，所以a2n=n．当2n-1=2009时，n=1005，故a2009+a2011=0．当2n=2010，a2010=1005．
解答 解：奇数项，偶数项分开看，
奇数项为1，-1，2，-2…，发现a2n-1+a2n+1=0，
偶数项为1，2，3…，所以a2n=n
当2n-1=2009时，n=1005，故a2009+a2011=0．
当2n=2010，a2010=1005．
∴a2009+a2010+a2011=1005．
故选：C
点评 本题考查数列的性质和应用，解题时要注意观察能力和分析能力的培养．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
17．某设备的使用年数x与所支出的维修总费用y的统计数据如下表：
根据上表可得回归直线方程为$\widehat{y}$=1.3x+$\widehat{a}$．若该设备维修总费用超过12万元就报废，据此模型预测该设备最多可使用10年．
| 使用年数x（单位：米） | 2 | 3 | 4 | 5 | 6 |
| 维修总费用y（单位：万元） | 1.5 | 4.5 | 5.5 | 6.5 | 7.5 |
20．已知集合{a，b，c}={0，1，2}，且下列三个关系：①a≠2；②b=2；③c≠0，有且只有一个正确，则100a+10b+c=（ ）
| A． | 12 | B． | 21 | C． | 102 | D． | 201 |
7．若离散型随机变量X的分布列为：
则实数a的值为$\frac{1}{5}$．
| X | 0 | 1 |
| P | 10a2-a | 2-6a |
17．△ABC的内角，角A，B，C的对边分别为a，b，c，已知，a=$\sqrt{5}，cosA=\frac{2}{3}$，c=2则b=（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | 3 |
4．
已知函数f（x）=ax3+bx2+c，其导函数f'（x）的图象如图，则函数f（x）的极小值为（ ）
已知函数f（x）=ax3+bx2+c，其导函数f'（x）的图象如图，则函数f（x）的极小值为（ ）| A． | c | B． | a+b+c | C． | 8a+4b+c | D． | 3a+2b |