题目内容
设直线2x+3y+1=0和圆x2+y2-2x-3=0相交于点A、B.
(1)求弦AB的垂直平分线方程;
(2)求弦AB的长.
(1)求弦AB的垂直平分线方程;
(2)求弦AB的长.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)根据圆的弦的性质可知,弦的垂直平分线过圆心,则问题可解;
(2)利用垂径定理去求即可.
(2)利用垂径定理去求即可.
解答:
解:(1)圆方程可整理为:(x-1)2+y2=4,圆心坐标为(1,0),半径r=2,
易知弦AB的垂直平分线l过圆心,且与直线AB垂直,
而kAB=-
,∴k1=
.
所以,由点斜式方程可得:y-0=
(x-1),
整理得:3x-2y-3=0.
(2)圆心(1,0)到直线2x+3y+1=0的距离为d=
=
,
故|AB|=2×
=
.
易知弦AB的垂直平分线l过圆心,且与直线AB垂直,
而kAB=-
| 2 |
| 3 |
| 3 |
| 2 |
所以,由点斜式方程可得:y-0=
| 3 |
| 2 |
整理得:3x-2y-3=0.
(2)圆心(1,0)到直线2x+3y+1=0的距离为d=
| |2+1| | ||
|
| 3 | ||
|
故|AB|=2×
22-(
|
2
| ||
| 13 |
点评:本题考查了直线与圆的位置关系中的相交弦问题,一般是利用几何法来解决.

练习册系列答案
相关题目
 如图,在正方体中,A、B为正方体的两个顶点,M、N、P为所在棱的中点,则异面直线MP、AB在正方体的正视图中的位置关系是( )
如图,在正方体中,A、B为正方体的两个顶点,M、N、P为所在棱的中点,则异面直线MP、AB在正方体的正视图中的位置关系是( )| A、相交 | B、平行 | C、异面 | D、不确定 |
已知点A(-4,0)和B(2,2)M是椭圆
+
=1上一动点,则|MA|+|MB|的最大值( )
| x2 |
| 25 |
| y2 |
| 9 |
A、10+2
| ||
B、
| ||
C、9+
| ||
D、9+2
|
已知x,y∈R+,且(x+1)(y+1)=4,则2x+y的最小值为( )
| A、3 | ||
| B、4 | ||
C、2
| ||
D、4
|
 如图,三棱柱ABC-A1B1C1中,侧棱AA⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点
如图,三棱柱ABC-A1B1C1中,侧棱AA⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点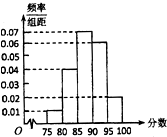 某次有1000人参加数学摸底考试,其成绩的频率分布直方图如题(16)图所示,规定85分及以上为优秀.
某次有1000人参加数学摸底考试,其成绩的频率分布直方图如题(16)图所示,规定85分及以上为优秀.
