题目内容
19.数列{an}中,已知对任意自然数n,a1+a2+a3+…+an=2n,则a12+a22+a32+…+an2=( )| A. | $\frac{1}{3}$(4n-1) | B. | $\frac{1}{3}$(2n-1) | C. | 4n-1 | D. | $\frac{1}{3}$(4n+8) |
分析 由题意求得数列{an}通项公式,则{an2}是从第二项起4为首项,4为公比的等比数列,利用等比数列的前n项和公式即可求得答案.
解答 解:当n=1时,可得a1=21=2,
当n≥2时,an=(a1+a2+…+an)-(a1+a2+…+an-1)
=2n-2n-1=2n-1,
当n=1时上式不成立,
∴an=$\left\{\begin{array}{l}{2}&{当n=1}\\{{2}^{n-1}}&{当n≥2}\end{array}\right.$,
当n≥2,∴$\frac{{a}_{n+1}^{2}}{{a}_{n}^{2}}$=$\frac{{2}^{2n}}{{2}^{2n-2}}$=4,
∴{an2}是从第二项起4为首项,4为公比的等比数列,
当n≥2时,a12+a22+a32…+an2=4+$\frac{4-{4}^{n}}{1-4}$=$\frac{1}{3}$(4n+8).
当n=1时,显然成立,
∴a12+a22+a32…+an2=$\frac{1}{3}$(4n+8).
故选D.
点评 本题考查等比数列前n项和的应用,考查等比数列通项公式的求法,考查分类讨论思想,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
14.来自英、法、日、德的甲、乙、丙、丁四位客人,刚好碰在一起,他们除懂本国语言外,每天还会说其他三国语言的一种,有一种语言是三人都会说的,但没有一种语言人人都懂,现知道:
①甲是日本人,丁不会说日语,但他俩都能自由交谈;
②四人中没有一个人既能用日语交谈,又能用法语交谈;
③甲、乙、丙、丁交谈时,找不到共同语言沟通;
④乙不会说英语,当甲与丙交谈时,他都能做翻译.针对他们懂的语言
正确的推理是( )
①甲是日本人,丁不会说日语,但他俩都能自由交谈;
②四人中没有一个人既能用日语交谈,又能用法语交谈;
③甲、乙、丙、丁交谈时,找不到共同语言沟通;
④乙不会说英语,当甲与丙交谈时,他都能做翻译.针对他们懂的语言
正确的推理是( )
| A. | 甲日德、乙法德、丙英法、丁英德 | B. | 甲日英、乙日德、丙德法、丁日英 | ||
| C. | 甲日德、乙法德、丙英德、丁英德 | D. | 甲日法、乙英德、丙法德、丁法英 |
4.已知{an}为等差数列,若a1+a2+a3=$\frac{π}{2}$,a7+a8+a9=π,则cosa5的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
9.已知$|{\overrightarrow a}|=6\sqrt{3},|{\overrightarrow b}|=\frac{1}{3}$,且$\overrightarrow a•\overrightarrow b=-3$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
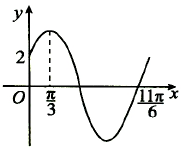 已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.