题目内容
20.已知$\overrightarrow{{e}_{1}}$=(1,0),$\overrightarrow{{e}_{2}}$=(0,1),$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数k=( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
分析 由已知向量的坐标求得$\overrightarrow{a}、\overrightarrow{b}$的坐标,然后利用向量共线的坐标运算求得答案.
解答 解:∵$\overrightarrow{{e}_{1}}$=(1,0),$\overrightarrow{{e}_{2}}$=(0,1),
∴$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$=(1,0)-2(0,1)=(1,-2),
$\overrightarrow{b}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$=k(1,0)+(0,1)=(k,1),
若$\overrightarrow{a}$∥$\overrightarrow{b}$,则1×1-(-2)×k=0,解得:k=$-\frac{1}{2}$.
故选:B.
点评 本题考查平面向量共线的坐标表示,关键是熟记有关公式,是基础的计算题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
5.两条直线a1x+b1y+c1=0与a2x+b2y+c2=0垂直的充要条件是( )
| A. | (-$\frac{{a}_{1}}{{b}_{1}}$)(-$\frac{{a}_{2}}{{b}_{2}}$)=-1 | B. | (a1,b1)•(a2,b2)=0 | ||
| C. | -$\frac{{a}_{1}}{{b}_{1}}$=$\frac{{b}_{2}}{{a}_{2}}$ | D. | a1b2=a2b1 |
10.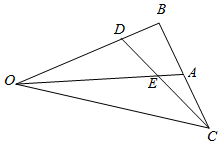 如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则三角形OEC与OBC的面积的比值是( )
如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则三角形OEC与OBC的面积的比值是( )
 如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则三角形OEC与OBC的面积的比值是( )
如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则三角形OEC与OBC的面积的比值是( )| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{8}$ |
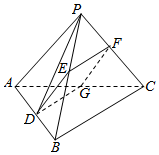 在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.
在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.