题目内容
9．直线方程Ax+By=0，若从0，1，3，5，7，8这6个数字中每次取两个不同的数作为A，B的值，则可表示22条不同的直线．分析 选中0时，Ax+By=0共能表达2条直线；当A、B从1，3，5，7，8五个数字中取值时，由排列组合的知识可得．
解答 解：第一类：当A或B中有一个取0时，另一个不论取何值，
方程都只能表示2条直线x=0和y=0．
即选中0时，Ax+By=0共能表示2条直线；
第二类，当A、B从1，3，5，7，8五个数字中取值时，共有C52=5×4=20，
综上所述，表示成不同直线的条数是2+20=22条
故答案为：22
点评 本题考查直线的一般式方程，解题时要注意分类讨论思想和排列组合知识的合理运用，属基础题
练习册系列答案
相关题目
20．已知$\overrightarrow{{e}_{1}}$=（1，0），$\overrightarrow{{e}_{2}}$=（0，1），$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$，若$\overrightarrow{a}$∥$\overrightarrow{b}$，则实数k=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 2 | D． | -2 |
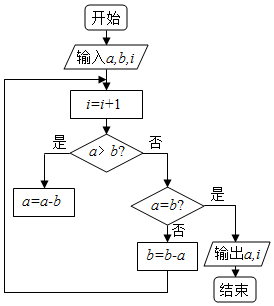如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b，i的值分别为12，16，0，则输出a和i的值分别为（ ）