题目内容
5.两条直线a1x+b1y+c1=0与a2x+b2y+c2=0垂直的充要条件是( )| A. | (-$\frac{{a}_{1}}{{b}_{1}}$)(-$\frac{{a}_{2}}{{b}_{2}}$)=-1 | B. | (a1,b1)•(a2,b2)=0 | ||
| C. | -$\frac{{a}_{1}}{{b}_{1}}$=$\frac{{b}_{2}}{{a}_{2}}$ | D. | a1b2=a2b1 |
分析 对b1,b2分类讨论,利用相互垂直的充要条件即可得出.
解答 解:b1b2≠0时,两条直线a1x+b1y+c1=0与a2x+b2y+c2=0垂直?$-\frac{{a}_{1}}{{b}_{1}}$$(-\frac{{a}_{2}}{{b}_{2}})$=-1,化为a1a2+b1b2=0.
b1b2=0时,且b1与b2不同时为0,也满足上式.
即满足条件:(a1,b1)•(a2,b2)=0.
故选:B.
点评 本题考查了直线相互垂直行的充要条件、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知$\overrightarrow{{e}_{1}}$=(1,0),$\overrightarrow{{e}_{2}}$=(0,1),$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数k=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
14.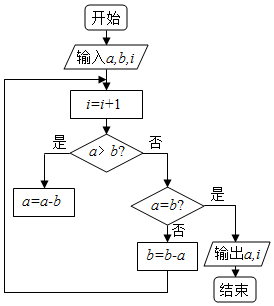 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为12,16,0,则输出a和i的值分别为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为12,16,0,则输出a和i的值分别为( )
 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为12,16,0,则输出a和i的值分别为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为12,16,0,则输出a和i的值分别为( )| A. | 4,3 | B. | 4,4 | C. | 4,5 | D. | 3,4 |
15.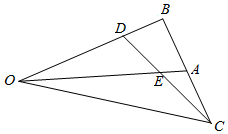 如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )
如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )
 如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )
如图:已知,在△OAB中,点A是BC的中点,点D是将向量$\overrightarrow{OB}$分为2:1的一个分点,DC和OA交于点E,则AO与OE的比值是( )| A. | 2 | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{6}{5}$ |