题目内容
11．
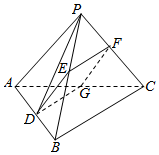在四面体PABC中，PA=PB=PC=5，AB=BC=AC=6，点E、F、G都是所在边的中点，E、F、G这三点所确定的平面与直线AB相交于点D．（1）证明：点D是线段AB的中点；
（2）求异面直线PD与BC所成的角的大小．
分析 （1）由已知得EF∥BC，从而BC∥平面EFG．从而DG∥BC．由此得到AD=DB，从而能证明点D是线段AB的中点．
（2）连PG，由（1）知DG∥BC，∠PDG的大小等于异面直线PD与BC所成角的大小或其补角的大小，由此能求出异面直线PD与BC所成的角大小．
解答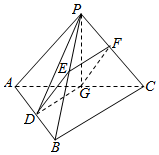 
证明：（1）∵PE=EB，PF=FC，∴EF∥BC，
∴BC∥平面EFG．
又由BC∥平面EFG，过BC作平面ABC与平面EFG相交交线为DG，
则DG∥BC．
∵AG=GC，∴AD=DB，点D是线段AB的中点．…（4分）
解：（2）连PG，由（1）知DG∥BC，
∠PDG的大小等于异面直线PD与BC所成角的大小或其补角的大小．…（6分）
在△PDG中，DG=3，$PD=PG=\sqrt{{5^2}-{3^2}}=4$，
$cos∠PDG=\frac{1.5}{4}=\frac{3}{8}$，$∠PDG=arccos\frac{3}{8}$．
∴异面直线PD与BC所成的角大小等于$arccos\frac{3}{8}$．…（8分）
点评 本题考查异面直线所成角的大小的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
1．2004 年世界卫生组织、联合国儿童基金会等机构将青蒿素作为一线抗疟药品推广．2015 年12 月10 日，我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖．目前，国内青蒿人工种植发展迅速．
某农科所为了深入研究海拔因素对青蒿素产量的影响，在山上和山下的试验田中分别种植了100 株青蒿进行对比试验．现在从山上和山下的试验田中各随机选取了4株青蒿作为样本，每株提取的青蒿素产量（单位：克）如表所示：
（Ⅰ）根据样本数据，试估计山下试验田青蒿素的总产量；
（Ⅱ）记山上与山下两块试验田单株青蒿素产量的方差分别为$s_1^2$，$s_2^2$，根据样本数据，试估计$s_1^2$与$s_2^2$的大小关系（只需写出结论）；
（Ⅲ）从样本中的山上与山下青蒿中各随机选取1 株，记这2 株的产量总和为ξ，求随机变量ξ的分布列和数学期望．
某农科所为了深入研究海拔因素对青蒿素产量的影响，在山上和山下的试验田中分别种植了100 株青蒿进行对比试验．现在从山上和山下的试验田中各随机选取了4株青蒿作为样本，每株提取的青蒿素产量（单位：克）如表所示：
| 编号 位置 | ① | ② | ③ | ④ |
| 山上 | 5.0 | 3.8 | 3.6 | 3.6 |
| 山下 | 3.6 | 4.4 | 4.4 | 3.6 |
（Ⅱ）记山上与山下两块试验田单株青蒿素产量的方差分别为$s_1^2$，$s_2^2$，根据样本数据，试估计$s_1^2$与$s_2^2$的大小关系（只需写出结论）；
（Ⅲ）从样本中的山上与山下青蒿中各随机选取1 株，记这2 株的产量总和为ξ，求随机变量ξ的分布列和数学期望．
2．已知函数f（x）=$\frac{x}{cosx}$，x∈（-$\frac{π}{2}，\frac{π}{2}$），当|xi|＜$\frac{π}{2}$（i=1，2，3）时，f（x1）+f（x2）＜0，f（x2）+f（x3）＜0，f（x3）+f（x1）＜0，则有（ ）
| A． | x1+x2+x3＞0 | B． | x1+x2+x3=0 | ||
| C． | x1+x2+x3＜0 | D． | x1+x2+x3的符号不能确定 |
20．已知$\overrightarrow{{e}_{1}}$=（1，0），$\overrightarrow{{e}_{2}}$=（0，1），$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$，若$\overrightarrow{a}$∥$\overrightarrow{b}$，则实数k=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 2 | D． | -2 |