题目内容
15.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若最初生产出的溶液含杂质2%,需要进行过滤,且每过滤一次可使杂质含量减少$\frac{1}{2}$,则要使产品达到市场要求至少应过滤5次.分析 设要使产品达到市场要求至少应过滤n次,由题意得$\frac{2}{100}×(\frac{1}{2})^{n}$≤$\frac{1}{1000}$,由此能求出结果.
解答 解:设要使产品达到市场要求至少应过滤n次,
由题意得$\frac{2}{100}×(\frac{1}{2})^{n}$≤$\frac{1}{1000}$,
∴($\frac{1}{2}$)n≤$\frac{1}{20}$,
∴n≥$\frac{lg\frac{1}{20}}{lg\frac{1}{2}}$=$\frac{1+lg2}{lg2}$≈4.3,
∵n∈N*,∴n=5.
故答案为:5.
点评 本题考查函数在生产生活中的实际应用,是中档题,解题时要认真审题,注意对数性质的合理运用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
5.口袋中有5个小球,其中两个黑球三个白球,从中随机取出两个球,则在取到的两个球同色的条件下,取到的两个球都是白球的概率( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
20.已知$\overrightarrow{{e}_{1}}$=(1,0),$\overrightarrow{{e}_{2}}$=(0,1),$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数k=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
7.已知i2=-1,复数z=i(1-i),则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
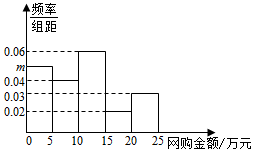 某调查机构从某县农村淘宝服务网点中随机抽取20个网点作为样本进行元旦期间网购金额(单位:万元)的调查.获得的所有样本数据按照区间[0,5],(5,10],(10,15],(15,20],(20,25]进行分组,得到如图所示的频率直方图
某调查机构从某县农村淘宝服务网点中随机抽取20个网点作为样本进行元旦期间网购金额(单位:万元)的调查.获得的所有样本数据按照区间[0,5],(5,10],(10,15],(15,20],(20,25]进行分组,得到如图所示的频率直方图