题目内容
某同学5次考试的成绩分别为x，y，100，110，90，已知这5次成绩的平均数为100，方差为200，则|x-y|的值为 ．
考点：极差、方差与标准差
专题：计算题,概率与统计
分析：利用平均数、方差的概念列出关于x，y的方程，设m=x-100，n=y-100，则m2+n2=800，m+n=0，即可得出结论．
解答：
解：由题意可得：x+y+100+110+90=500，
∴x+y=200，
根据方差公式得（x-100）2+（y-100）2+100+100=1000，
设m=x-100，n=y-100，则m2+n2=800，m+n=0，
∴|m-n|=|x-y|=40，
故答案为：40．
∴x+y=200，
根据方差公式得（x-100）2+（y-100）2+100+100=1000，
设m=x-100，n=y-100，则m2+n2=800，m+n=0，
∴|m-n|=|x-y|=40，
故答案为：40．
点评：本题考查统计的基本知识，样本平均数与样本方差的概念以及求解方程组的方法，比较简单．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
数列{an}中，a1=1，an+1+an=（-1）n•2n（n∈N*，n≥1），Sn是数列{an}的前n项和，则S10=（ ）
| A、682 | B、-682 |
| C、62 | D、-62 |
如图：样本A和B分别取自两个不同的总体，他们的样本平均数分别为
A和
B，样本标准差分别为sA和sB，则（ ）
. |
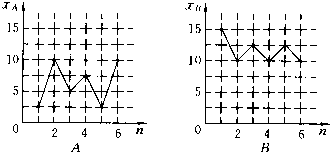
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|