题目内容
为弘扬“乐于助人,与人为善”中华传统美德,某社区组织了一个40人的社区志愿者服务团队,他们在一个月内参加社区公益活动的次数统计如表所示:
(1)从该服务团队中任意选3名志愿者,求这3名志愿者中至少有两名志愿者参加活动次数签好相等的概率;
(2)从该服务团队中任选两名志愿者,用X表示这两人参加活动次数只差的绝对值,求随机变量X的分布列及数学期望E(X).
| 活动次数 | 1 | 2 | 3 |
| 参加人数 | 5 | 15 | 20 |
(2)从该服务团队中任选两名志愿者,用X表示这两人参加活动次数只差的绝对值,求随机变量X的分布列及数学期望E(X).
考点:离散型随机变量的期望与方差
专题:计算题,概率与统计
分析:(1)利用对立事件的概率公式,可得这3名志愿者中至少有两名志愿者参加活动次数签好相等的概率;
(2)由题意知X的可能取值是0,1,2,由题设条件分别求出P(X=0),P(X=1)和P(X=2)的值,由此能求出X的分布列及数学期望E(X).
(2)由题意知X的可能取值是0,1,2,由题设条件分别求出P(X=0),P(X=1)和P(X=2)的值,由此能求出X的分布列及数学期望E(X).
解答:
解:(1)利用对立事件的概率公式,可得这3名志愿者中至少有两名志愿者参加活动次数签好相等的概率为
1-
=
;
(2)X的可能取值为0,1,2,则
P(X=0)=
=
,P(X=1)=
=
,P(X=2)=
=
,
X的分布列为
∴EX=0×
+1×
+2×
=
.
1-
| ||||||
|
| 419 |
| 494 |
(2)X的可能取值为0,1,2,则
P(X=0)=
| ||||||
|
| 61 |
| 156 |
| ||||||||
|
| 75 |
| 156 |
| ||||
|
| 5 |
| 39 |
X的分布列为
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 61 |
| 156 |
| 75 |
| 156 |
| 5 |
| 39 |
| 115 |
| 156 |
点评:本题考查离散型随机变量的分布列和数学期望,考查概率的求法和应用,是历年高考的必考题型.解题时要认真审题,仔细解答.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
如果袋中有6个红球,4个白球,从中任取1球,记住颜色后放回,连续摸取4次,设ξ为取得红球的次数,则Eξ为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读如图所示的程序框图,若输入的k=6,则输出的值S是( )


| A、63 | B、64 |
| C、127 | D、128 |
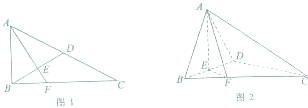 如图1,在Rt△ABC中,∠ACB=30°,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2所示.
如图1,在Rt△ABC中,∠ACB=30°,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2所示.