题目内容
设底面直径和高都是4厘米的圆柱的内切球为O．
（1）求球O的体积和表面积；
（2）与底面距离为1的平面和球的截面圆为M，AB是圆M内的一条弦，其长为2
，求AB两点间的球面距离．
（1）求球O的体积和表面积；
（2）与底面距离为1的平面和球的截面圆为M，AB是圆M内的一条弦，其长为2
| 3 |
考点：球的体积和表面积,多面体和旋转体表面上的最短距离问题
专题：计算题,空间位置关系与距离
分析：（1）求出球O的半径，即可求球O的体积和表面积；
（2）求出∠AOB=
，可得AB两点间的球面距离．
（2）求出∠AOB=
| 2π |
| 3 |
解答：
解：（1）∵底面直径和高都是4厘米的圆柱的内切球为O，
∴球O的半径为2cm，
∴球O的体积为
π•23=
，表面积4π•22=16π；
（2）∵AB是圆M内的一条弦，其长为2
，
∴∠AOB=
，
∴AB两点间的球面距离为
．
∴球O的半径为2cm，
∴球O的体积为
| 4 |
| 3 |
| 32π |
| 3 |
（2）∵AB是圆M内的一条弦，其长为2
| 3 |
∴∠AOB=
| 2π |
| 3 |
∴AB两点间的球面距离为
| 4π |
| 3 |
点评：本题考查AB两点间的球面距离，考查球O的体积和表面积，确定球的半径是关键．
练习册系列答案
相关题目
阅读如图所示的程序框图，若输入的k=6，则输出的值S是（ ）
| A、63 | B、64 |
| C、127 | D、128 |
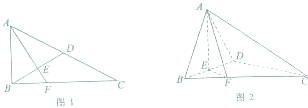如图1，在Rt△ABC中，∠ACB=30°，∠ABC=90°，D为AC中点，AE⊥BD于E，延长AE交BC于F，将△ABD沿BD折起，使平面ABD⊥平面BCD，如图2所示．
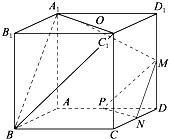如图，在正方体ABCD-A1B1C1D1中，M、N、P分别为所在边的中点，O为面对角线A1C1的中点．