题目内容
10.在区间[-1,5]上随机地取一个实数a,则方程x2-2ax+4a-3=0有两个正根的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{3}$ |
分析 根据根与系数之间的关系,求出a的取值范围,结合几何概型的概率公式进行计算即可.
解答 解:若方程x2-2ax+4a-3=0有两个正根,
则满足$\left\{\begin{array}{l}{△=4{a}^{2}-4(4a-3)=4({a}^{2}-4a+3)≥0}\\{4a-3>0}\\{2a>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a≥3或a≤1}\\{a>\frac{3}{4}}\\{a>0}\end{array}\right.$,得$\frac{3}{4}$<a≤1或a≥3,
∵-1≤a≤5
则对应的概率P=$\frac{1-\frac{3}{4}}{5-(-1)}$+$\frac{5-3}{5-(-1)}$=$\frac{1}{24}$+$\frac{1}{3}$=$\frac{3}{8}$,
故选:C
点评 本题主要考查几何概型的概率的计算,根据根与系数之间的关系求出a的取值范围是解决本题的关键.

练习册系列答案
相关题目
15.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(1)求回归直线方程$\stackrel{∧}{y}$=bx+a,其中b=-20,a=$\overline{y}$-b$\overline{x}$;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
回归直线的斜率和截距的最小二乘估计公式分别为$\stackrel{∧}{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$.
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
回归直线的斜率和截距的最小二乘估计公式分别为$\stackrel{∧}{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$.
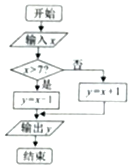 已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.