题目内容
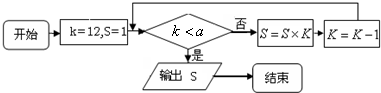
程序框图如图：如果上述程序运行的结果为S=132，那么判断框中实数a的取值范围是 ．
考点：程序框图
专题：算法和程序框图
分析：执行程序框图，当K=11时，有S=132；当K=10时满足条件k＜a，输出S的值为132，即有10＜a≤11．
解答：
解：执行程序框图，有
k=12，S=1
不满足条件k＜a，有S=12，K=11；
不满足条件k＜a，有S=132，K=10；
满足条件k＜a，输出S的值为132．
即有10＜a≤11，
故答案为：（10，11]．
k=12，S=1
不满足条件k＜a，有S=12，K=11；
不满足条件k＜a，有S=132，K=10；
满足条件k＜a，输出S的值为132．
即有10＜a≤11，
故答案为：（10，11]．
点评：本题主要考察了程序框图和算法，属于基础题．
练习册系列答案
相关题目
在△ABC中，根据下列条件解三角形，则其中有两个解的是（ ）
| A、b=10，A=45°，C=75° |
| B、a=7，b=5，A=80° |
| C、a=60，b=48，C=60° |
| D、a=14，b=16，A=45° |
已知集合A={1，2，3，4}，B={a，b，c}，f：A→B为集合A到集合B的一个函数，那么该函数的值域C的不同情况有（ ）
| A、7种 | B、4种 | C、8种 | D、12种 |
已知P={-1，0，
}，Q={y|y=sinθ，θ∈R}，则P∩∁RQ=（ ）
| 2 |
| A、∅ | ||
B、{
| ||
| C、{-1，0} | ||
D、{-1，0，
|
下列结论错误的是（ ）
| A、命题：“若a＞b＞0，则a2＞b2”的逆命题是假命题 | ||||||||
| B、若函数f（x）可导，则f′（x0）是x0为函数极值点的必要不充分条件 | ||||||||
C、向量
| ||||||||
| D、命题p：“?x∈R，ex≥x+1”的否定是“?x∈R，ex＜x+1” |